Абстрактный и конкретный синтаксис
При рассмотрении приемов программирования и примеров на разных языках необходимо как можно больше отвлекаться от частных особенностей и учиться видеть за ними общее с тем, чтобы оставшиеся различия были бы уже принципиальными. Отделить существенное от несущественного помогает, в частности, соотношение между синтаксисом и семантикой. Например, оказывается, что некоторые синтаксические особенности КС-грамматики языка не нужны для описания его семантики.
Обычное синтаксическое определение языка задает конкретные синтаксические правила построения программы как строки символов. При этом определяется, какие структурные элементы могут быть выделены в тексте программы (конкретное представление программы).
Действия абстрактного вычислителя определяются на структурном представлении программы и не зависят от многих особенностей конкретного синтаксиса. Например, для присваивания важно лишь то, что в нем есть получатель и источник, сам по себе знак присваивания (=, := или, скажем, LET) совершенно не важен. Более того, неважно, в каком порядке расположены составные части присваивания в тексте программы. Например, конструкция языка COBOL
MOVE X+Y TO Z
выражающая присваивание получателю Z значения выражения X+Y, совершенно аналогична обычному оператору присваивания.
Для того, чтобы четко отличать конкретное представление от существенной структуры, стоит рассматривать конкретный и абстрактный синтаксис. Скажем, абстрактный синтаксис всех перечисленных форм операции присваивания один и тот же.
Аналогично, три оператора
X = a * b + c * d; X = (a * b) + (c * d); (4.1) X = ((a * b) + (c * d));
и подобные им полностью эквивалентны с точки зрения абстрактного синтаксиса, тогда как с точки зрения текстового представления — различны.
Таким образом, нужна структура синтаксических понятий, которая соответствует некоторому алгоритмически разрешимому8) (см., напр. [20]) понятию эквивалентности программ. Но это понятие эквивалентности должно быть исключительно простым, поскольку теоретические результаты показывают, что нетривиальные понятия эквивалентности программ неразрешимы.
Выбранное понятие эквивалентности определяет структурное представление синтаксиса, используемого для задания абстрактного вычислителя (абстрактно-синтаксическое представление).
Фрагментом абстрактно-синтаксического представления является чаще всего применяемый на практике ход. Задают понятие синтаксической эквивалентности, которое очевидным образом согласуется с функциональной эквивалентностью. Так, например, предложения, перечисленные в примере 4.1, могут описываться следующим понятием синтаксической эквивалентности: скобки вокруг подвыражений, связанных операцией более высокого приоритета, чем операция, примененная к их результату, могут опускаться. В данном смысле присваивание рассматривается как операция, имеющая более низкий приоритет, чем любая из арифметических операций. Таким образом, например, определяется эквивалентность выражений в языке Prolog. Подвыражение X + 3, скажем, является в нем всего лишь другим вариантом записи для +(X,3), и при вычислении характеристик выражения оно прежде всего преобразуется в форму без знаков операций.
Еще одну возможность, открываемую переходом к абстрактно-синтаксическим определениям, можно увидеть, если определить эквивалентность подвыражений для сложения и умножения
A + B - B + A.
Здесь абстрактная эквивалентность выражает свойство самой операции. Опыт показывает, что дальше учета ассоциативности и коммутативности в абстрактном синтаксисе двигаться весьма опасно.
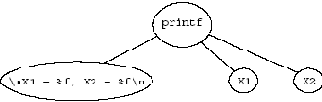
Рис. 4.1. Оператор печати
Пример на рис. 4.1 иллюстрирует вызов функции:
printf ("\nX1 = %f, X2 = %f\n", X1, X2);
Показанная на рисунке структура абстрактного синтаксиса данного оператора показывает, как можно ликвидировать привязку конструкции языка к конкретному синтаксису: остались только имя функции, строка и два параметра.
Рассмотрим более сложный пример, показывающий родство абстрактного синтаксиса традиционных языков. На рис. 4.2 показано абстрактное представление фрагмента текста следующей программы:
. . . if ( D > 0 ) { D = sqrt ( D );
Пример 4.5.1.
Текст некоторой программы
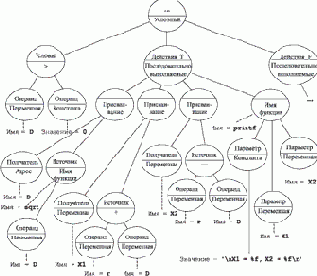
Рис. 4.2. Представление фрагмента текста программы
 |
 |
 |
Язык программирования и алгоритмический язык почти всегда являются синонимами. В данном пособии они синонимичны.
2)
Нельзя абсолютизировать это требование. Совместные вычисления могут производиться в неизвестном программисту порядке. Более того, автору известен случай, когда прагматика (системы Common Lisp) четко отмечает, что в некотором случае нельзя пользоваться конкретным линейным порядком, который система порождает, пополняя заданный пользователем частичный порядок зависимостей, поскольку алгоритм упорядочивания может быть в любой момент и без предупреждения заменен. На самом деле такая прагматика часто полностью соответствует содержательному смыслу создаваемых программ: если два действия независимы, нельзя предполагать, что одно из них происходит раньше другого (хотя обычно программист вынужден это предполагать ввиду идиотизма "современных" систем). Если бы такие прагматические замечания встречались почаще!
3)
Поскольку синтаксис порою (особенно раньше) отождествлялся с контекстно-свободной его частью, в литературе иногда можно встретить термин "статическая семантика" для описания контекстных зависимостей. Вспоминая определение семантики, мы видим, что такой термин вводит в заблуждение.
4)
Даже возможная противоречивость библиотек друг другу соответствует стилю содержательного мышления (И.Н. Скопин).
5)
Вообще говоря, данная подсказка избыточна для современных трансляторов, поскольку распознать шаблон вида <переменная> ":=" <переменная /* та же самая */> "+" 1 и им подобные не представляет труда не только в тех случаях, когда <переменная> указана явно, но и тогда, когда она вычисляется (индексирование, косвенная адресация и т. д.).
6)
Сегодня с помощью семантической прагматики выражают также расширения модели вычислений, выводящие за рамки исходного абстрактного исполнителя. К примеру, — системы параллельного программирования над C++ и FORTRAN MPI и OPEN MP (И. Н. Скопин).
7)
Модель вычислений препроцессора можно охарактеризовать следующими свойствами. Исходные перерабатываемые данные — это текст (любой структуры, не обязательно на языке С), в котором имеются строки, начинающиеся с символа '#'. Такие строки представляют команды, управляющие работой препроцессора. Например, #include . . . заставляет препроцессор вставить некоторый файл в перерабатываемый текст (не следует понимать это буквально — нужно просто обеспечить соответствующий эффект). Другой пример: #define two 2 дает указание препроцессору на то, что в оставшейся части текста идентификатор two должен заменяться числом 2. Результат вычислений препроцессора — текст, который не содержит его команд.
8)
Как принято в современной теории, "алгоритмически разрешимое" далее называется просто "разрешимое".

