Общие концепции
Язык логического программирования PROLOG представляет собой одну из моделей сентенциального программирования. Мы используем лишь те возможности языка PROLOG, которые согласуются с принятым в 1996 г. стандартом [36]. Как руководство по программированиюна языке PROLOG можно использовать, скажем, книгу [6]. В ней содержится наименьшее число недочетов и откровенных ошибок, а также наибольшее число практических советов по сравнениюс другими известными автору пособиями.
Первой находкой создателей языка PROLOG явилось понятие унификации, изобретенное в методе резолюций для доказательства формул классической логики предикатов.
Два выражения называются унифицируемыми, если они могут быть приведены к одному и тому же виду подстановкой значений вместо свободных переменных. Унификация—вид конкретизации, при котором границы всех синтаксических единиц фиксированы, структура выражения однозначно определена и подстановка, приводящая два выражения к одному и тому же виду, вычисляется рекурсивно.
Второй находкой, перенесенной авторами языка PROLOG из специализированных программ (для логики и искусственного интеллекта) в языки программирования, стала система обработки неудач. Успешно произведенная унификация является лишь разрешением выполнить некоторое действие. После проверки других условий, возможно, мы будем вынуждены вернуться и выбрать другой вариант.
Третья находка языка PROLOG, перенесенная в программирование из метода резолюций, — это стандартизация цели. Целью доказательства в методе резолюций всегда является получение пустого дизъюнкта, то есть стирание доказываемого выражения (с логической точки зрения, приведение его к абсурду). Точно так же и в языке PROLOG: успешное исполнение программы означает стирание поля зрения.
Четвертая находка создателей языка PROLOG взята из ограничения классической логики. Хорновские формулы
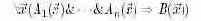
обладают важным свойством. Для нахождения вывода в системе хорновских формул достаточно производить так называемую линейную резолюцию, когда на каждом шаге делается вывод из исходной формулы и наследника цели. Никаких сочетаний исходных формул между собой либо различных вариантов раскрытия цели между собой делать, в принципе, не нужно.
