Управление исполнением программы
Джулией Робинсон доказано (см., напр. [30]), что для выражений первого порядка имеется эффективный алгоритм унификации, находящий для двух выражений унифицирующую подстановку либо обосновывающий, что такой подстановки нет.
Пример 6.3.1. Две последовательности выражений
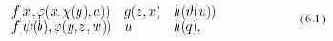
где a, b — константы, а латинские буквы из конца алфавита — переменные, унифицируются в
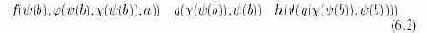
подстановкой

А в двух последовательностях

никакие два соответственных выражения унифицированы быть не могут.
Уже в приведенном примере видно, что унификация — глобальная операция.
Заметим, что логический алгоритм унификации обладает свойством частичного исполнения: если унифицировать две подструктуры, то после исполнения унифицирующей подстановки можно продолжить унификацию остальных подструктур, и результат унификации не изменится. Так что выражения могут унифицироваться одно за другим5).
Рассмотрим, как исполняется программа на языке PROLOG. В программе может быть одно целевое предложение, не имеющее головной части. Оно начинается с функтора :- или ?-. В программе, транслируемой и исполняемой в пакетном режиме, обычно используется первый функтор, а при задании цели с терминала в режиме диалога—второй. Разница между ними проявляется лишь в режиме диалога. Второй вариант цели позволяет пользователю после нахождения одного из решений продолжить выполнение программы для поиска следующего решения. Первый такой возможности ему не представляет, программа находит какое-нибудь решение и останавливается.
Исходная цель называется запросом. Переменные, входящие в запрос, носят особый статус. Их значения в ходе последовательных унификаций накапливаются в скрытой части поля памяти программы и при успешном исполнении выдаются в качестве ответа на запрос.
В каждый момент рассматривается первый из термов цели. Если его детерминатив не является встроенной функцией или встроенным оператором с особым определением, то ищется предложение, голова которого унифицируется с этим термом. При этом прежде всего проверяется наличие предложений, детерминатив которых совпадает с детерминативом первого терма.
Если таких предложений несколько, то создается точка возврата, в которой запоминается состояние программы для отработки возможных неудач.
Предложения испытываются, начиная с первого. Полученная унифицирующая подстановка применяется ко всем термам в поле зрения и к хвосту успешно унифицированного предложения. После этого хвост заменяет унифицированную голову, и выполнение возобновляется. Исполнение считается успешным, если на некотором шаге цель исчезает. Исполнение считается неудачным, если в некоторый момент для первого из термов не найдется унифицируемого с ним предложения.
Заметим, что переменные предыдущих унификаций отождествляются с переменными следующих унификаций лишь в том случае, если эти переменные дожили в поле зрения до соответствующей унификации. Если переменная уже получила постоянное значение либо значение, в котором она не встречается, то в последующем переменные с тем же именем трактуются как новые. Таким образом, конкретные имена переменных имеют значение лишь внутри одного предложения.
Если исполнение оказалось неудачным, то программа возвращается к последней из точек возврата (происходит откат) и испытывается следующее по порядку предложение с тем же детерминативом. Если таких предложений больше не осталось, то происходит откат к следующей точке возврата, и так далее. Если исполнение откатилось до запроса и больше кандидатов на унификацию не осталось, программа заканчивается общей неудачей.
Стандартным ответом программы на запрос служит Yes, если программа закончилась удачно, и No, если она закончилась неудачно. При удаче выводятся значения всех переменных исходного запроса.
Так, например, если программа и ее база данных имеют вид
greater(X,Y):-greater1(X,Y). greater(X,Y):-greater1(Z,Y),greater(X,Z). greater1(X,f(X)). estimation(X,Y):-greater(X,Y),known(Y). known(f(f(f(f(a))))). unknown(a). unknown(b).
Пример 6.3.1.
то ответом на запрос
?-unknown(Y),estimation(Y,X).
будет
Y=a X=(f(f(f(f(a)))) Yes
а при попытке ответа на запрос
?-estimation(b,X).
программа зациклится.
Насколько каверзны вроде бы невинные предположения (например, условие, что подцели достигаются строго одна за другой и варианты перебираются в том же порядке), сделанные в языке PROLOG, видно из того, что при логически эквивалентной переформулировке одного из предложений программы
estimation(X,Y):-known(Y),greater(X,Y).
программа успешно ответит на второй запрос
No
Еще более впечатляющий пример рассмотрен в упражнении 5.
Есть еще одна особенность языка PROLOG, которая кажется явным ляпсусом, но на самом деле является отражением результата Косовского и др. (неизвестного реализаторам и пользователям языка PROLOG, но лучшими из них ощущаемого интуитивно) о несовместимости моделей отождествления PROLOG и Рефала. Вся работа системы PROLOG основана на предположении, что значения унифицируемых переменных набираются однозначно, и следующий вариант может получиться лишь в результате унификации с другим фактом либо предложением. Поэтому когда (как в случае со списками или строками) PROLOG встречается с неоднозначным отождествлением, он никогда не будет перебирать разные его варианты. Он либо выберет первый из них (например, при унификации неизвестных [X|Y] с уже известным списком Z X будет пустым списком), либо зациклится на бесконечном повторении одного и того же варианта (смотри предыдущую скобку, которая иллюстрирует сразу две неприятности: если к такой унификации вернутся, будет выбран 'новый' пустой список в качестве X).
Для того, чтобы вычислить выражение, имеется предопределенная бинарная операция is. Она должна иметь вторым аргументом выражение, составленное из атомов при помощи функций. После применения X is 1+2 вместо X подставится 3. Даже выражение 1+2 остается в таком же виде, пока оно не попадет во второй аргумент is.
Внимание!
То, что некоторый функтор определен как операция, не значит, что он вычисляется. Это просто изменение конкретно-синтаксического представления. Для того чтобы иметь возможность вычислить выражение, нужно определить функтор как внутреннюю или внешнюю функцию.
При этом необязательно делать его операцией.
Рассмотренные до сих пор средства языка PROLOG не дают возможности сформулировать отрицание. Впрочем, отрицание и не может присутствовать в хорновых формулах, его наличие разрушает свойства, которые послужили основой для модели вычислений языка PROLOG. Но на практике оно нужно, и поэтому в языке PROLOG введен его суррогат. Этот суррогат дает возможность программисту минимально управлять точками возврата. Если в цели встал на первое место атом ! (называемый предикатом отсечения), то он успешно унифицируется и уничтожает последнюю точку возврата. Предикат ! используется прежде всего для определения отрицания как явного неуспеха подцели.
Пример 6.3.2. Рассмотрим, как с помощью ! и списков программируется поиск пути в лабиринте (и даже в произвольном ориентированном графе).
way(X,X,[X]). way(X,Y,[Y|Z]):-connect(U,Y), nomember(Y,Z),way(X,U,Z). way(X,Y,[Y|Z]):-connect(U,Y), way(X,U,Z). nomember(Y,Z):-member(Y,Z),!,fail. nomember(Y,Z). connect(begin,1). connect(1,begin). connect(1,2). connect(2,3). connect(3,1). connect(3,4). connect(4,end).
Листинг 6.3.2. Статический лабиринт
В ответ на запрос
?-way(begin,end,X).
программа выдаст
X = [end, 4, 3, 2, 1, begin] Yes
Вместо определения nomember можно написать предложение
way(X,Y,[Y|Z]):-connect(U,Y),not (member(Y,Z)),way(X,U,Z).
Предикат отсечения можно использовать для того, чтобы превратить PROLOG-программу в программу с традиционным управлением, оставив из специфики языка лишь операцию унификации. На практике и при обучении часто бывают случаи, когда кому-нибудь никак не удается совладать с PROLOG и отладить свою программу, поскольку он зациклен на императивном стиле программирования. Узнав о !, он облегченно вздыхает и переписывает свою программу таким образом, что она становится изоморфной программе в обычном языке программирования. Как правило, при такой трансформации теряются главные преимущества языка PROLOG, но зато сохраняются все его недостатки.
Внимание!
Некоторые из русскоязычных учебных пособий по языку PROLOG написаны людьми, не понимающими сути других стилей программирования. Видимым признаком такого пособия может служить постоянное использование отсечений.
Прагматические соглашения о порядке выполнения действий в программе привели к тому, что если мы запишем в форме языка PROLOG тривиальную тавтологию
A:-A.
и этот оператор6) выполнится, то программа зациклится. И по этой причине, и по причине ошибки в унификации предложения языка PROLOG, сохранив внешнюю форму логических, по существу отношения к логике уже не имеют.
Конечно же, несообразности были использованы и для получения новых эффектов. Рассмотрим следующее определение.
repeat. repeat:-repeat.
Если вставить теперь цель repeat в раскрытие другой цели и позаботиться о том, чтобы последующие подцели в большинстве случаев заканчивались неудачей, а после удачи поставить !, то эти подцели будут повторяться вплоть до удачи и их побочные эффекты будут исполняться в цикле.
Приведенное выше определение repeat писать в программах не нужно. В стандарте PROLOG задан встроенный предикат repeat, потенциально бесконечное число раз успешно унифицируемый. Реализованный в языке PROLOG перебор вариантов при всех своих недостатках довольно удачно моделирует недетерминированные алгоритмы в программе.
Недетерминированную модель вычислений, соответствующую PROLOG, можно определить в общем виде следующим образом:
- Имеются точки разветвления, допускающие переходы без проверки условий выбора вариантов — точки недетерминированного разветвления.
- Вычислительный процесс выбирает в такой точке любое из возможных продолжений.
- Некоторые из возможных продолжений объявляются тупиковыми, или тупиками, т. е. такими, которые не приводят вычислительный процесс к заранее определенной цели. Принципиально, что тупик продолжения не может определиться в точке разветвления.
- Успешным вычислением называется такая последовательность выбираемых продолжений в каждой точке недетерминированного разветвления, которая приводит процесс к цели (т.
е. ни одно из выбранных продолжений не является тупиком).
Недетерминированным достижением цели называется успешное вычисление. Таким образом, если какая-то из последовательностей продолжений приводит к цели, то цель процесса считается достигнутой. Недетерминированная модель вычислений может применяться и как средство декомпозиции решаемой задачи, когда программист просто откладывает 'на потом' вопрос, как будет организован перебор вариантов.
Есть теорема, доказывающая, что в принципе недетерминированный конечный автомат всегда можно преобразовать в детерминированный. Идея преобразования — склейка состояний, как показано на рис. 6.1. При этом, содержательно говоря, мы создаем линейный порядок на множестве альтернатив и выбираем альтернативы в строгом соответствии с этим порядком. Именно так с самого начала поступили в языке PROLOG. Беды в этом нет. В то время, когда создавался язык PROLOG, идея совместности (т. е. безразличия некоторых последовательностей предложений к порядку их исполнения) и недетерминированности (т. е. ситуации, когда один и тот же оператор в одном и том же контексте может давать разные результаты) как положительного фактора была только что осознана. А те, кто делают что-либо принципиально новое, почти всегда забывают согласовать свою находку с другими принципиальными достижениями того же времени, предпочитая локализовать новизну и в остальных пунктах работать как можно более традиционно. Беды начались, когда особенности конкретного упорядочивания стали беспощадно использоваться в хакерском духе, да еще и выставляться как принципиальные новации.
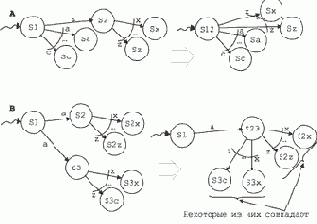
Рис. 6.1. Преобразование недетерминированного поиска в детерминированный
Теорема детерминирования конечного автомата обосновывает существование успешного вычисления. Но она не дает никаких хороших оценок изменения сложности вычислений при переходе к детерминированному поиску. И даже если успешное вычисление существует, это не означает, что трансформировать ассоциированные с переходами действия легко и что после трансформации они будут хоть сколько-нибудь понимаемы.По этой причине часто обработку удобнее описывать как недетерминированную, поручая решение задачи организации перебора вариантов системе программирования.
