Модель вычислений LISP
Для LISP (как и для любого другого функционального языка) не обязательно2) говорить, где и как размещаются структуры данных (списки).
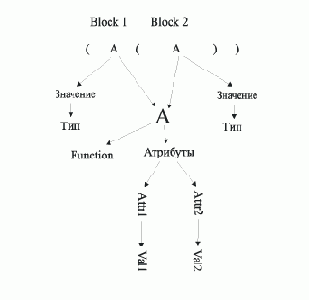
Рис. 8.1. Структура информации, сопоставленной атому языка LISP
Их стоит рассматривать как сугубо математические объекты со сложной структурой, которая всегда точно указывает на текущие вычислительные элементы:
- До выполнения шага вычисления — это список, включающий имя функции и ее аргументы.
- Во время выполнения шага вычисления — это те фрагменты списочной структуры поля зрения, которые доступны для использования вычисляемой функцией (в частности, среди них есть список, связанный с именем функции, который определяет ее вычислительный процесс).
- После выполнения шага вычислений — это результаты вычислений. Результаты можно разделить на три группы:
- значение, выдаваемое вызовом функции: оно замещает в поле зрения отработанный вызов функции;
- побочные эффекты, разбросанные по структуре поля данных;
- очередная функция, которая будет вычисляться далее. В традиционном программировании обычно возвращаются к вычислениям той функции, которая активизировала завершаемую. В функциональном программировании может быть и по-другому. Результат может оказаться функцией, либо описанной в статическом тексте программы, либо скомпонованной в ходе вычислений.
Общую структуру данных и программы функционального языка можно рассматривать как связный нагруженный граф, динамически изменяющийся в ходе вычислений, у которого имеются активные вершины, т. е. функции, вычисляемые в данный момент, потенциально активные вершины, соответствующие функциям, которым назначено вычисление или продолжение вычисления (отложенного, приостановленного и т. п.), и пассивные вершины, участие которых в вычислениях в данный момент не запланировано. Дуги графа отмечают связи по управлению или по данным между функциями. Такой граф далее называется абстрактным графом функциональных вычислений.
Конкретизировать такой граф и стратегию отработки активных вершин можно разными способами.
При этом могут появляться разные ипостаси функционального программирования.
Для абстрактного вычислителя граф функциональных зависимостей естественно считать полем памяти функциональной программы, в котором выделено поле зрения: активные (либо активные и потенциально активные) вершины-функции со своими аргументами.
В практике реализации функциональных систем программирования имеется три варианта конкретизации представления графа:
- Списки LISP, которые связаны с последовательными вычислениями. Структура графа задается как совокупность линейных списков, объединяющих имена функций и указатели аргументов. Голова списка трактуется как указание функции, а хвост — как аргументы.
- Коммутационные схемы, которые строятся на основе разделения функций и данных: функции представляются вершинами графа, а их аргументы-данные передаются по дугам, соединяющим вершины. Дуги рассматриваются в качестве каналов связи. Функция активизируется, когда ее аргументы появляются в каналах.
- Ассоциативные схемы, в которых вершины-функции остаются виртуальными. Они образуются в результате связывания данных, имеющих одинаковый ключ. Ситуация, когда такие данные появляются в ассоциативной памяти, трактуется как готовность аргументов для вычисления функции, идентифицируемой этим ключом.
Коммутационные и ассоциативные схемы рассмотрены при обсуждении неимперативных моделей вычислений (см. § 1.2 и 3.1). Выбор последовательно просматриваемой структуры для первого функционального языка обусловлен единственной для того времени возможностью реализации функциональности путем моделирования ее операционными средствами традиционной модели вычислений. Списочная структура также строится посредством более или менее стандартного для традиционной модели адресного представления. С языковой точки зрения именно этот выбор обеспечивает однородность структуры программы и данных, на базе которой Дж. Маккарти удалось построить систему средств, достаточную для практического функционального программирования.
Программа на языке LISP задается как список применений функций, часть из которых может вычисляться во время исполнения самой программы.
Как правило, заданные в программе списки интерпретируются как применения функций и вычисляются, если другое не определяют ранее активированные функции (вы видели, что функция quote запрещает вычисление своего аргумента, функция setq запрещает вычисление лишь первого из двух аргументов, а функция setf заставляет вычислить первый аргумент лишь до стадии, когда получена ссылка на его значение). Любое выражение выдает значение, что используется, в частности, при диалоговой работе с LISP (на примере которой иллюстрируются понятия).
Основные управляющие функции концептуально едины и позволяют динамически строить блочную структуру программы. В частности, функция
(block name e1 . . . en) (8.1)
вычисляет свои аргументы, начиная со второго, один за другим, тем самым задавая последовательность команд. Первый ее аргумент, name, служит именем блока. В любой момент из любого объемлющего блока можно выйти и выдать значение с помощью функции
(return-from name value) (8.2)
Этим LISP выгодно отличается от большинства языков, где такие структурные переходы либо неполны, либо некорректно реализованы.
Далее, блоком считается любое описание функции. Описание функции производится при помощи функции defun, которая, в свою очередь, определяется через примитивы function и lambda. Первый из них задает, что имя, являющееся его аргументом, рассматривается как функция (он часто сокращается в конкретном синтаксисе до #’), второй образует значение функционального типа. Имя функции является и именем функционального блока.
Пример 8.4.1. В данном примере иллюстрируются определение факториала, вызов анонимной функции и возможность вычисления произвольного функционального выражения, созданного в программе.
[1]> (defun fact (n) (if (= n 0) 1 (* (fact (- n 1)) n))) FACT [2]> (fact 40) 815915283247897734345611269596115894272000000000 [3]> ((lambda (x) (fact (* x x))) 5) 15511210043330985984000000 [4]> (setq g ’(lambda (x) (fact (* x x)))) (LAMBDA (X) (FACT (* X X))) [5]> (eval (list g 3)) 362880
Нужно заметить, что определение функции с данным именем и значение имени могут задаваться независимо. Например, мы можем в этом же контексте задать (setq fact 7), хотя, конечно же, это отвратительный способ программирования.
Все формальные параметры функций являются локальными переменными. Никакие изменения их значений не выходят наружу. Но все другие свойства остаются глобальными! Приведем пример.
[23]> (defun f (x) (progn (setf (get ’x ’weight) ’(25 kg)) (+ x 3))) F [24]> (setf (get ’x ’weight) ’(30 kg)) (30 KG) [25]> (get ’x ’weight) (30 KG) [26]> (setq x 5) 5 [27]> (f 3) 6 [28]> x 5 [29]> (get ’x ’weight) (25 KG)
В LISP имеется возможность создать анонимный блок со своими локальными переменными, не объявляя его функцией. Создание такого блока называется связыванием переменных и производится функцией let.
Значение имени, унаследованного извне, все равно будет внешним! Смотрите пример ниже.
[32]>(setq a ’(b c d)) (B C D) [33]>(setq b 5) 5 [34]> (list (let ((b 6)) (eval (car a))) (eval (car a))) (5 5) [35]> (list (let ((b 6)) b) (eval (car a))) (6 5) [36]> (list (let ((b 6)) (list b a)) (eval (car a))) ((6 (B C D)) 5) [37]> (list (let ((b 6)) (eval (car (list ’b a)))) (eval (car a))) (5 5)
Важнейшей особенностью функционального программирования как стиля, впервые использованной в языке LISP, являются функционалы с аргументами-функциями. Рассмотрим пример возведения всех членов кортежа в квадрат.
[57]> (setq a (list 1 5 7 9 11 13 15 19 22 28)) (1 5 7 9 11 13 15 19 22 28) [58]> (mapcar (function (lambda (x) (* x x))) a) (1 25 49 81 121 169 225 361 484 784)
Функционал mapcar применяет свой первый аргумент ко всем членам второго.
Такие функционалы, в частности, делают циклы практически ненужными. Тем не менее в языке LISP есть конструкции циклов как дань программистской традиции. Чужеродность циклов подчеркивается тем, что они всегда выдают значение NIL.
И, наконец, приведем пример3).
Пример 8.4.2. Данная программа строит автомат для нахождения всех вхождений некоторой системы слов во входной поток.
Позже она анализируется с точки зрения автоматного программирования.
;================================================== ; ; свертка/развертка системы текстов ; текст представлен списком ;((Имя Вариант ...)...) ; первое имя в свертке - обозначение системы текстов ; (Элемент ...) ; (Имя Лексема (Варианты)) ; ((пример (ма (ш н) ; (ш а) ) ; ( ш н ) ) ; ((н ина)) ) ;================================================== ; реализация свертки: unic, ass-all, swin, gram, bnf
(defun unic (vac) (remove-duplicates (mapcar ’car vac) )) ;; список уникальных начал
(defun ass-all (Key Vac) ;; список всех вариантов продолжения ( что может идти за ключом) (cond ((Null Vac) Nil) ((eq (caar Vac) Key) (cons (cdar Vac) (ass-all Key (cdr Vac)) )) (T (ass-all Key (cdr Vac)) ) ) )
(defun swin (key varl) (cond ;; очередной шаг свертки или снять скобки при отсутствии вариантов ((null (cdr varl))(cons key (car varl))) (T (list key (gram varl)) ) ))
(defun gram (ltext) ;; левая свертка, если нашлись общие начала ( (lambda (lt) (cond ((eq (length lt)(length ltext)) ltext) (T (mapcar #’(lambda (k) (swin k (ass-all k ltext ) )) lt ) ) ) ) (unic ltext) ) )
(defun bnf (main ltext binds) (cons (cons main (gram ltext)) binds)) ;; приведение к виду БНФ
;=================================================== ; реализация развертки: names, words, lexs, d-lex, d-names, ; h-all, all-t, pred, sb-nm, chain, level1, lang
(defun names (vac) (mapcar ’car vac)) ;; определяемые символы
(defun words (vac) (cond ;; используемые символы ((null vac) NIL) ((atom vac) (cons vac NIL )) (T (union (words(car vac)) (words (cdr vac)))) ))
(defun lexs (vac) (set-difference (words vac) (names vac))) ;; неопределяемые лексемы
(defun d-lex ( llex) ;; самоопределение терминалов (mapcar #’(lambda (x) (set x x) ) llex) ) (defun ( llex)
;; определение нетерминалов (mapcar #’(lambda (x) (set (car x )(cdr x )) ) llex) )
(defun h-all (h lt) ;; подстановка голов (mapcar #’(lambda (a) (cond ((atom h) (cons h a)) (T (append h a)) ) ) lt) )
(defun all-t (lt tl) ;; подстановка хвостов (mapcar #’(lambda (d) (cond ((atom d) (cons d tl)) (T(append d tl)) ) ) lt) )
(defun pred (bnf tl) ;; присоединение предшественников (level1 (mapcar #’(lambda (z) (chain z tl )) bnf) ))
(defun sb-nm (elm tl) ;; постановка определений имен (cond ((atom (eval elm)) (h-all (eval elm) tl)) (T (chain (eval elm) tl)) ) )
(defun chain (chl tl) ;; сборка цепочек (cond ((null chl) tl) ((atom chl) (sb-nm chl tl))
((atom (car chl)) (sb-nm (car chl) (chain (cdr chl) tl) ))
(T (pred (all-t (car chl) (cdr chl)) tl)) ))
(defun level1 (ll) ;; выравнивание (cond ((null ll)NIL) (T (append (car ll) (level1 (cdr ll)) )) ))
(defun lang ( frm ) ;; вывод заданной системы текстов (d-lex (lexs frm)) (d-names frm) (pred (eval (caar frm)) ’(()) ) )
Листинг 8.4.1. Автомат для нахождения всех вхождений некоторой системы слов во входной поток
