Взаимодействие процессов и распараллеливание

До сих пор мы рассматривали идеальный случай, когда процессы независимы между собой и вопрос об их взаимодействии возникает лишь в момент их завершения. Но на практике так конечно же бывает крайне редко. Процессы практически всегда взаимосвязаны, и поэтому нужно рассмотреть вопрос об организации связей между ними.

Первая связь - общие данные. Рассмотрим самый простой случай, когда у процессов есть общее поле памяти, в которое они записывают обновленные данные и читают их в случае необходимости. Даже в этом случае возникают сложности. Если один из процессов начал обновлять данные в поле, а другой как раз в это время их читает, то может случиться так, что он получит мешанину из старых и обновленных данных (такой случай в распределенных системах и в базах данных рассматривается как нарушение целостности данных1)).

Здесь следует ввести понятие критического интервала, когда программа, занимающая некоторый ресурс, должна быть уверена в том, что никто больше к этому ресурсу обратиться не может, что ее работающие в параллель "друзья" не могут навредить либо не будут дезориентированы.

Конечно, проще всего установить монопольное использование общего ресурса: программа, обратившаяся к этому ресурсу, устанавливает флаг, и пока флаг поднят, никто другой обратиться к нему не может. Но представьте себе, например, коллективную работу над пухлым техническим заданием. Мне нужно, скажем, внести изменения в главу 3, а я не могу сделать этого, поскольку уже пару часов некто корпеет над главой 13, которая практически от главы 3 не зависит. В этом случае прибегают к корпоративным системам поддержки распределенной работы (в качестве положительного примера устойчиво работающей системы можно привести Lotus Works, правда, с 2002 г. автор с ней не работал, так что улучшения, сделанные с тех пор, могли повлечь потерю надежности). В них решаются тонкие задачи поддержания целостности данных при поступлении изменений из множества источников, при сбоях серверов, сети и т.п. Все это делается таким образом, чтобы работа одного из сотрудников практически не мешала работе других (а если уж мешает, значит, оба пытаются залезть в одно и то же место, но для этих случаев предусмотрена система развязки конфликтов).

Второй вид связи параллельных процессов - критические точки. Когда процесс достиг критической точки, это означает, что он может двигаться дальше лишь в том случае, если другие процессы также достигнут соответствующей критической точки. Например, для вычисления следующей итерации необходимо убедиться в том, что предыдущая итерация уже всеми закончена. Для следующего поиска необходимо узнать, что хотя бы один из параллельно работающих процессов уже нашел предыдущие данные.

Есть один важный частный случай &-параллелизма, когда критические точки и критические интервалы не вызывают проблем. Это - конвейерный параллелизм. При конвейерном параллелизме основную часть времени процессы работают независимо. Затем работа всех частных процессов приостанавливается, происходит обмен данными и просмотр происшедших событий. Такая организация работы аналогична заводскому конвейеру: пока конвейер стоит, рабочие выполняют свои операции; затем конвейер движется, передавая результаты операций следующему исполнителю.

Это было неформальное введение в теоретические тонкости, возникающие при взаимодействии процессов (все равно, действительно параллельных или квазипараллельных). А на практике часто важнее другие детали.

Хорошее распараллеливание невозможно без подробного анализа программы. В самом деле, если один из процессоров несет 99% вычислительной нагрузки, то мы на распараллеливании лишь прогадаем, поскольку добавятся накладные расходы на синхронизацию процессов. Так что первая проблема практического распараллеливания - предсказание сложности вычислений различных блоков программы. Только если удается равномерно распределить вычисления по процессорам, причем такая равномерность должна сохраняться внутри каждого интервала между взаимодействиями процессов, распараллеливание дает выигрыш. В параллельном программировании автор наблюдал примеры, когда вроде бы безобидное и абсолютно корректное с точки зрения обычного программирования улучшение одного из блоков приводило к ухудшению работы всей программы.

Так что оптимизация не всегда монотонна по отношению к разбиению на подсистемы.

Теперь рассмотрим один из методов квазипараллельного программирования, зачастую хорошо подходящий для моделирования естественного параллелизма автоматного программирования и потенциального параллелизма событийного программирования. Это моделирование в системе с логическим дискретным временем.

Концепция времени является одной из важнейших во многих областях. Более того, в известном американском афоризме Time is money абсолютная ценность низводится до уровня условной. Время мы не можем получить ни от кого, не можем сохранить, можем лишь тратить.

При компьютерном моделировании поведения объектов целесообразно выделить два аспекта:

образы действующих объектов;
моделирование времени.

Если время не моделируется, а берется из реального мира, говорят о системах реального времени. Если же время является частью виртуального мира системы, то это - логическое время. Выделяя его прикладные аспекты, часто говорят о логическом времени как об условном, или модельном, времени.

Рассмотрим тот простейший (но исключительно важный) случай времени, когда время может быть представлено как линейно упорядоченная совокупность шагов, а все процессы, протекающие между шагами, можно считать неделимыми. Тогда на временной оси у нас есть лишь дискретная совокупность точек, в которых нужно поддерживать целостность системы и каждого из процессов. Такая дисциплина возможна и для систем реального времени, если допустима некоторая задержка ответа на событие (такой случай называется мягким реальным временем). Тогда можно дождаться естественного завершения шага нашего процесса и лишь в промежутке между шагами просматривать события.

Если время является не только дискретным, но и логическим, то говорят о системе с дискретными событиями. Эта ситуация хорошо подходит для применения и моделирования как конвейерного, так и

-параллелизма.

Пример 15.3.2. Рассмотрим модельную задачу. Пусть нужно найти кратчайший путь в нагруженном ориентированном графе, где каждая дуга оснащена числом, интерпретируемым как ее длина.

Это традиционно интерпретируется как определение кратчайшего пути между городами A и B, связанными сетью однонаправленных дорог.

Покажем, что решение задачи можно построить как систему взаимодействующих процессов с дискретным временем. Это - хороший метод структурирования задачи и отделения деталей от существенных черт: сначала мы строим абстрактное представление, а затем конкретизируем его, например укладывая, по сути своей, параллельный алгоритм в рамки последовательной программы3). Идея этого подхода восходит к У.-И. Далу и Ч. Хоору, которые использовали данную задачу для демонстрации возможностей системы с дискретными событиями, предоставляемой языками SIMULA 60 и SIMULA 67, совпадавшими по модели времени и структуре управления процессами.

Базовой концепцией в данной задаче естественно является

-параллелизм. Определение кратчайшего расстояния можно представить как соревнование действующих агентов4) , "разбредающихся" по разным дорогам. Сразу же разграничиваются два класса алгоритмов: прямые, когда общий процесс начинается с A, и обратные, для которых стартовым городом назначается B. Для показа принципиальных моментов достаточно рассмотреть по одному прямому и обратному алгоритму.

Прямой алгоритм разбредающихся агентов можно описать как поведение каждого агента по следующей схеме, в качестве параметра которой задается местонахождение агента:

Если агент стоит в городе, то
- Если местонахождение агента есть B, то цель достигнута. В качестве результата выдается пройденный путь.
- Агент проверяет, является ли город запретным. Если это так, агент ликвидируется (понятно, что при этом информация по системе в целом не теряется - другие агенты продолжают действовать).
- Город, в котором стоит агент, объявляется запретным.
- Порождается столько наследников агента, сколько дорог исходит из текущего местонахождения данного агента. При этом в качестве локальных данных новых агентов задается пройденный путь, запомненный родительским агентом от A до текущего местонахождения (не принципиально, уничтожается ли родительский агент или он становится одним из экземпляров наследников).
  
  Если нет дорог из текущего местонахождения, то агент ликвидируется - он зашел в тупик.
Переход к следующему моменту времени - для каждого агента осуществляется один шаг передвижения по текущей дороге. Это можно интерпретировать как задержку выполнения программы на время, необходимое для перемещения в свой следующий пункт (мерой времени в данном случае служит расстояние между пунктами).
Осуществляется переход к пункту 1.

Видно, что алгоритм завершает работу, когда найден путь из A в B либо когда все агенты оказываются ликвидированы.

Как и обычно, более жесткие условия на окончательную программу влекут за собой во многих отношениях более мягкие требования к прототипу (нужно расширить возможности его перестройки в разные варианты окончательной программы), но при этом желательно максимально возможное повышение уровня понятий прототипа. Если в конце концов программа будет реализована квазипараллельно, не нужно обращать внимание на то, сколько агентов могут действовать одновременно. В частности, в случае заведомого наличия пути из A в B можно не проверять запретность либо ослабить ее до случая, когда предок данного агента посещал данный город, и, следовательно, он оказался на запомненном пути. В этом случае не потребуется запоминание глобальной, а точнее, общей для всех агентов информации о графе дорог и городов.

Приведенный алгоритм нуждается в запоминании сведений о пройденном пути в локальных данных агентов. Таким образом, локальные данные каждого из агентов, которые будут ликвидированы, хранятся напрасно. Если же их забывать, то искомый путь не может быть получен, получаются лишь некоторые его характеристики. Этого недостатка лишено решение с помощью обратного блуждания, т.е. от B к A. Для него все работает точно так же, за исключением следующего:

локальная информация об агентах и их путях не запоминается;
в качестве пометки о посещении указывается, из какого города агент пришел в данный город (это можно называть пометкой-рекомендацией).

В результате, когда какой-либо из агентов достигнет A, последовательность, начинающаяся с A и выстраивающаяся по пометкам-рекомендациям, дает искомый путь.

Рис. 15. 2 иллюстрирует работу всех трех алгоритмов: прямого (a), прямого с пометками (b) и обратного с пометками-рекомендациями (c). Надписи на дугах-дорогах обозначают агентов, верхние индексы на них - порядок порождения агентов. В косых скобках записаны локально хранимые сведения о посещаемых городах. Зачеркнутые надписи указывают на уничтожение агента в связи с использованием сведений о посещениях городов.

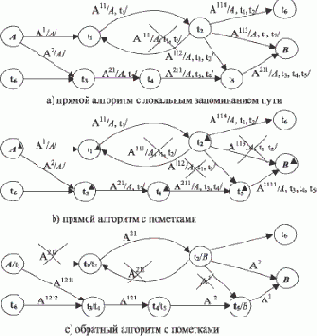
Рис. 15.2. Логика алгоритмов поиска пути

Как прямой, так и обратный алгоритмы работоспособны, если обеспечить одновременную работу сразу всех процессов агентов. Если вычислитель дает возможность многопроцессорной обработки, причем с потенциально неограниченным5) числом процессоров, то это условие выполнено автоматически.

Если параллелизм возможен, но процессов недостаточно (например, если Вы решите воспользоваться для реализации этих алгоритмов Prolog-системой Muse), то мы находимся в трудной ситуации, требующей творческих решений, комбинации научного и инженерного подхода6).

Возникает вопрос о средствах эмуляции дискретных событий. Имеются пакеты работы с дискретными событиями, но еще в 60-е гг. было показано, что мышление в терминах времени на самом деле требует собственного языка. Классическим примером здесь до сих пор является язык SIMULA 67. Он в явном виде провозглашает имитацию параллелизма и, следовательно, дает человеку возможность мыслить в терминах действующих агентов, что представляется более гибким и естественным способом выражения многих алгоритмов. Систему с дискретными событиями можно рассматривать в качестве общего метода преодоления противоречия между принципиальным параллелизмом и реальной последовательностью вычислений.

Классическая реализация систем с дискретными событиями - это общая среда поддержки процессов. Каждый процесс может находиться в одном из четырех состояний, которые определяются с использованием так называемого управляющего списка: строго упорядоченной очереди процессов, назначаемых на выполнение. В хорошей реализации классической модели этот список скрыт.

Для каждого процесса определяется структура данных, достаточная для полного запоминания его состояния в момент, когда дискретный шаг закончен7). Запомненное состояние называется точкой возобновления.

Состояние называется:

активным, когда (реально) выполняется программа процесса;
приостановленным, когда выполнение программы процесса прервано, но запомнена точка возобновления и процесс находится в управляющем списке;
пассивным, когда процесс не выполняется и не находится в управляющем списке, но точка возобновления активности запомнена;
завершенным, когда выполнение его программы прервано и точка возобновления активности не запомнена.

Конструкция управляющего списка имитирует время. Первый процесс всегда активный. Это единственный активный процесс. Если он прерывает свое выполнение, то активным становится следующий за ним приостановленный процесс. Процесс может быть вставлен в управляющий список (перед каким-либо процессом в списке или после него, через определенное время) или удален из него. Процесс также может быть назначен на определенное время, он вставляется перед тем процессом, время выполнения которого минимально превосходит назначаемое. Возможно случайное (псевдослучайное) действие по вставке процесса в то или иное место управляющего списка.

Можно считать, что с помощью управляющего списка процессам задаются относительные приоритеты.

Постулируется, что все оперирование с управляющим списком и с состояниями активности процессов является следствием событий, дискретно происходящих в системе. Пока какое-либо из событий не произошло, состояние процесса и его положение в управляющем списке не могут изменяться.

Видно, что это имитационная модель, создающая структуру, для внешнего наблюдателя практически неотличимую от реального параллелизма, причем с неограниченным количеством процессоров. Поскольку у нас система с дискретными событиями, время логическое и временные задержки являются лишь средством перестройки управляющего списка.

Как следует из перечисленного выше, применительно к решаемой задаче копирование агентов означает:

создание локальных структур данных агентов-процессов;
размещение агентов-процессов в управляющем списке;
перемещение каждого активного агента- процесса по управляющему списку на величину времени его задержки;

Согласно постулату о событиях выполнение любого процесса-агента не может привести к изменению планируемого порядка выполнения остальных процессов, пока не произойдет событие. В данном случае событиями являются истечение временной задержки, а также самоликвидация активного агента, в результате которой активным становится следующий процесс управляющего списка.

К примеру, для обратного алгоритма с пометками-рекомендациями схема программы агента, пришедшего в город, сводится к следующему:

Выждать время, необходимое для перемещения из местоположения в данный город (фактически, это означает лишь соответствующую перестановку себя в управляющем списке, сопровождающуюся приостановкой процесса);
Если данный город уже посещался (в городе имеется пометка-рекомендация), то ликвидировать себя, т.е. завершить процесс;
Сделать пометку-рекомендацию в данном городе, используя местоположение, из которого пришел агент;
Если данный город есть A, то построить путь, используя пометки рекомендации, и завершить процесс;
Для каждой дороги, ведущей в данный город, породить процесс нового агента, в качестве параметра которого задается данный город. Назначить активизацию нового процесса непосредственно после прекращения активности родительского процесса;
Завершить процесс.

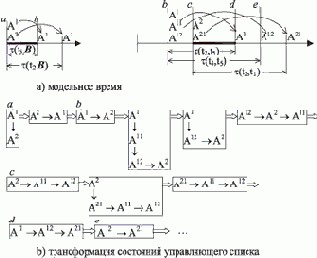
Рис. 15.3. Управляющий список

На рис. 15.3 изображено начало последовательности состояний управляющего списка, которая получается при выполнении алгоритма с данными, представленными на рис. 15.2с. В верхней части рисунка изображена модель времени: на горизонтальной оси отмечены моменты, когда состояние агентов меняется (? - функция времени перемещения между городами; a, b, c и d - моменты для дальнейшего пояснения). В нижней части рисунка показана последовательность изменений управляющего списка (его состояния выделены прямоугольными блоками, в которых для наглядности вертикальные стрелки обозначают связи процессов, назначенных на одно и то же время, а горизонтальные стрелки - упорядоченность процессов по модельному времени).

Разбредание агентов начинается с порождения процессов A1 и A2, что соответствует двум дорогам, ведущим в город B. Это момент модельного времени, помеченный как a. Моменту b соответствуют четыре состояния, сменяющие друг друга, c соответствуют три, а d - одно состояние. Из сопоставления рисунков 15.2a и 15.2b видно, что никакого специального моделирования времени, а тем более задержек не требуется: время изменяется "мгновенно", когда все события, назначенные к более ранним срокам, отработали и в голове управляющего списка появляется событие, назначенное на более поздний срок. В принципе, здесь не требуется даже атрибут времени - достаточно отношения порядка между событиями.

Даже зацикливание некоторых агентов не помешает выполнению алгоритма, если только вместимость управляющего списка будет достаточной.

Необходимо подчеркнуть ряд важных моментов:

Реального параллелизма в системе с дискретными событиями нет, но есть эффект параллелизма, который лишен многих самых неприятных особенностей, требующих специальной заботы о синхронизации.
Изначально в каждый момент набор одновременно действующих агентов упорядочен частично, он становится упорядоченным полностью за счет соответствующей расстановки в управляющем списке.
Управляющий список - общая структура данных для агентов-процессов, но ее нельзя считать глобальной, так как явного доступа управляющий список не имеет.

В качестве хорошего изложения современного состояния дел в технике практического параллельного программирования можно рекомендовать книгу [14]. В частности, и система MPI, описанная в указанной книге, и ныне весьма широко и необоснованно рекламируемая система Open MP включают в себя средства квазипараллельного исполнения параллельных программ, отличные от системы с дискретными событиями. Эти средства мы не описываем, поскольку для реальных программ они нужны лишь как метод отладки параллельных программ на машине с недостаточной конфигурацией (причем метод, не вызывающий особых восторгов).

1)

Имеются и другие случаи нарушения целостности данных, мы показали лишь простейший из возникающих при совместной работе.

2)

Поведение русских абсолютно противоположное.

3)

Поскольку здесь мы переходим от сравнительно идеальных к низкоуровневым понятиям, такая задача избавления от совместности методологически и практически правильно поставлена, в отличие от задачи распараллеливания.

4)

В данном случае для подчеркивания специфики экземпляры объектов лучше называть так.

5)

По крайней мере, с заведомо большим, чем нужно для данной задачи.

6)

Когда математику приносят задачу о расчете устойчивости стола с четырьмя ножками, он быстро выдает результаты для стола с одной и с бесконечным числом ножек, а затем долго пытается точно решить конкретную задачу.

7)

Вспомните, что в системах с дискретными событиями целостность данных должна гарантироваться лишь в момент между шагами процесса.

Содержание раздела