Альтернативные обозначения для математических формул
Наряду со стандартными TeX'овскими обозначениями для математических формул, LaTeX предоставляет альтернативные обозначения. Именно, внутритекстовую формулу, которая в стандартных обозначениях ограничивается одним знаком доллара в начале и одним в конце, можно вместо этого заключить в знаки "\(" (в начале) и "\)" (в конце):
 | \(2\times2=4\) |
Другой вариант обозначений для внутритекстовой формулы, предоставляемый LaTeX'ом, — написать \begin{math} в начале формулы и \end{math} в конце (иными словами, внутритекстовая формула может быть оформлена как окружение с именем math).
Выключную формулу LaTeX позволяет окружить с обеих сторон не только парами знаков доллара, как предусмотрено стандартом, но знаками \[ (в начале) и \] (в конце). Кроме того, можно оформить выключную формулу как окружение с именем displaymath. В одном и том же файле можно использовать как стандартные, так и LaTeX'овские обозначения для формул.
Эти альтернативные обозначения полностью эквивалентны стандартным TeX'овским (со знаками доллара), за одним важным исключением: если выключные формулы обозначаются LaTeX'овскими, а не TeX'овскими обозначениями, то можно сделать так, что выключные формулы будут не центрированы, а прижаты влево .
Чего мы еще не сказали
Для читателя-математика того, что мы уже рассказали о наборе формул, должно быть, в принципе, достаточно, за одним важным исключением: при написании математической статьи полезно знать, как грамотно оформлять тексты теорем, определений и тому подобные вещи. Об этом у нас рассказывается в разд."Окружение типа "теорема","Окружение типа "теорема" в пакете amsthm" лекции 7 вы можете прочитать это уже сейчас, пропуская непонятные места и справляясь при необходимости с разд."Рубрикация документа" лекции 4, посвященным рубрикации документа.
Фантомы и прочее
Ранее мы столкнулись с командой \lefteqn, позволяющей напечатать фрагмент формулы и при этом сообщить TeX'у, что отдельного места (по горизонтали) на этот фрагмент отводить не надо. Иногда бывает полезно сделать обратное: включить в формулу символ, который сам не печатается, но место занимает. Вот пример такой ситуации.
Команда \sqrt автоматически выбирает размер знака радикала таким образом, чтобы он точно соответствовал высоте подкоренного выражения, и это очень хорошо. Иногда, однако, такой автоматический выбор приводит к не очень удачным результатам:
 | В формуле $\sqrt{a}+ \sqrt{d}$ два знака радикала имеют разные размеры. |
Дело тут, конечно, в том, что буквы




 | В формуле $\sqrt{\mathstrut a} +\sqrt{\mathstrut d}$ оба знака радикала имеют одинаковые размеры. |
Точнее говоря, \mathstrut - это невидимый символ, равный по высоте скобке

Невидимый символ, создаваемый командой \mathstrut, является частным случаем TeX'овской конструкции "фантома". Именно, если в формуле вы напишете
"\phantom{"TeXtit{какая-то формула} "}"то результат будет такой же, как если бы эта самая "какая-то формула" была сначала напечатана по всем правилам TeX'а, а затем аккуратно стерта с бумаги. Пример:
 | Все мы знаем, что знак радикала выглядит так: $\sqrt{\phantom{x}}$. |
Кроме того, можно создать "вертикальный фантом" формулы (по вертикали будет оставлено столько же места, сколько занимала бы формула, по горизонтали вертикальный фантом места не занимает).
Создается вертикальный фантом командой \vphantom. В частности, команда \mathstrut - это сокращение для "\vphantom{(}" . Возможны, наконец, и горизонтальные фантомы, занимающие по горизонтали столько же места, сколько заняла бы формула, и не занимающие места по вертикали. Создаются они командой \hphantom:
 | На пустое место $\hphantom{\sin^2\alpha}$ можно вписать формулу вручную. |
 | $$ \lefteqn{\overbrace{ \phantom{1+2+3}}} 1+\underbrace{2+3+4} $$ |




Если бы формула была не выключная, а внутритекстовая, то этот трюк прошел бы не столь гладко. Дело в том, что команда \lefteqn всегда набирает формулы в \displaystyle, поэтому размер фантома, над которым ставилась скобка, мог в принципе не совпасть с размером реально печатаемого фрагмента формулы. Чтобы уж совсем себя обезопасить, следовало бы в этом случае аргумент команды \lefteqn начать с \textstyle.
Формула в рамочке
Очень важную формулу хочется взять в рамку. Если подключить пакет amsmath, то этого можно добиться с помощью команды \boxed:
 | $$ \boxed{\iint_{\mathbb R^2}e^{-(x^2+y^2)}\,dx\,dy=\pi} $$ |
В этом примере мы подразумевали, что подключен еще пакет amsfonts или amssymb.
Горизонтальные отбивки вокруг формул
Некоторые авторы и издатели считают, что математический текст выглядит понятнее, когда каждая формула окружена дополнительным пробелами справа и слева от нее {Это актуально для текстов на языках с латинской графикой. В русских текстах формулы обычно достаточно выделяются уже за счет того, что в них используется латиница, а в тексте — кириллица.}. Для этих целей в TeX'е предусмотрен параметр \mathsurround . Значение этого параметра — размер дополнительного пробела, вставляемого по обе стороны каждой внутритекстовой математической формулы (этот пробел не добавляется перед формулой, попавшей при печати в начало строки, и после формулы, попавшей в конец строки). При запуске LaTeX'а значение этого параметра равно нулю, так что расстояния между формулами и окружающим текстом такие же, как между словами в тексте. Можно, однако, присвоить параметру \mathsurround ненулевое значение. Например, команда \mathsurround=2pt (будучи включена в преамбулу) окружает каждую формулу дополнительными пробелами по 2 пункта с обеих сторон.
Если нужно организовать дополнительные горизонтальные отбивки вокруг какой-то одной формулы, можно поместить команду, присваивающую значение параметру \mathsurround, непосредственно в саму формулу (между ограничивающими ее знаками доллара, в любое место). Важно только не забыть сделать пробел после обозначения для единицы длины (скажем, pt).
 |
 |
 |
2) Иногда полезно поставить пустые фигурные скобки {\{\}}, чтобы создать фиктивный аргумент бинарной операции и тем самым обеспечить желательные пробелы; мы делали это в примере на с.38

Какие еще есть символы
В наших таблицах собрано более четырехсот математических символов, не считая операций типа


Как набирать формулы
О некоторых простейших приемах набора формул уже шла речь в первой лекции, но для серьезной работы этого, бесспорно, недостаточно; хочется верить, что после изучения этой лекции профессиональному математику (или техническому редактору) не будет страшна никакая, даже самая изощренная, формула.
Некоторые из приемов, описываемых здесь, становятся доступными только после подключения специальных стилевых пакетов. Напомним, что слова наподобие "чтобы сделать то-то и то-то, надо подключить стилевые пакеты yweird и queer" означают, что в преамбулу документа следует включить строчку вида
\usepackage{weird,queer}Особенно полезны возможности, предоставляемые пакетами amssymb и amsmath, рекомендуем подключать их всегда, если в вашем тексте присутствуют сколько-нибудь сложные формулы.
Имея все это в виду, приступим к делу.
Многострочные выключные формулы
Программа TeX никогда не делает автоматических переносов в выключных формулах, поэтому, если ваша формула не умещается в строку, необходимо разбить ее на отдельные строки самостоятельно. Первое, что приходит в голову начинающим, — это оформить каждую из этих строк как отдельную выключную формулу с помощью $$...$$ и записать эти выключные формулы подряд. При этом расстояние по вертикали между двумя строками получается слишком большим, так что на глаз они не воспринимаются как части одной формулы. В этом разделе мы описываем, как грамотно организовать такое разбиение.
Как и в случае с матрицами, наиболее удобные (и рекомендуемые нами) средства открываются, если подключить пакет amsmath; с их описания мы и начнем, а в конце опишем скромные средства набора многострочных формул, доступные без подключения дополнительных пакетов.
Итак, пусть вы подключили amsmath. Тогда самое простое средство для набора многострочных выключных формул — это окружение multline:
 | \begin{multline} 1+2+3+4+\ldots\\ +46+47+48+\ldots\\ +99+100=5050 \end{multline} |
Первая из строк печатается выключенной влево, последняя — выключенной вправо, остальные строки центрируются. Подобно окружению equation, окружение multline не должно быть заключено в знаки "$$". Как вы могли заметить, формула, оформленная в виде окружения multline, автоматически нумеруется. Чтобы этой нумерации не было, надо воспользоваться "вариантом со звездочкой" — окружением multline*.
На самом деле первая и последняя строки печатаются не вплотную к полям, а с отступом, равным \multlinegap. Значение этого параметра можно изменить обычным образом, написав в преамбуле что-нибудь вроде
\multlinegap=.5inЧтобы какая-то из средних строк была не центрирована, а выключена влево, надо воспользоваться командой \shoveleft, написав, скажем,
\shoveleft{+46+47+48+\ldots}\\вместо "+46+47+48+\ldots\\". Для выключки вправо аналогичным образом используется команда \shoveright.
Когда несколько выключных формул идут подряд, можно не оформлять каждую из них с помощью "$$" или окружения equation, но воспользоваться окружением gather:
 | \begin{gather} 2\times 2=4\\ 9\times 9=81 \end{gather} |
p> При использовании gather формулы также не должны быть заключены в символы "$$". Каждая из формул, собранных в gather, автоматически нумеруется. Чтобы на пронумерованную таким образом формулу можно было сослаться (а иначе зачем нумеровать?), надо ее пометить, поставив перед |\\| команду \label.
Если какую-то из них нумеровать не надо, следует поставить непосредственно перед "\\" команду \notag. Если вы не хотите нумеровать ни одну из формул, можно воспользоваться "вариантом со звездочкой" — окружением gather* .
При разбиении выключной формулы на части нередко бывает желательно расположить строки одна под другой так, чтобы они были определенным образом выровнены. Для достижения такого эффекта удобно воспользоваться окружением split:
 | \begin{equation} \begin{split} 1999&=1000+900+{}\\ &+90+9 \end{split} \end{equation} |
Формулы, разбитые на части с помощью split , можно использовать также внутри окружений gather или align (о последнем речь пойдет ниже), со звездочками или без.
Нередко возникает необходимость напечатать один или несколько выровненных столбцов формул. Для этих целей предназначено окружение align:
 | \begin{align} 7\times 9& =63 & 63:9& =7\\ 9\times 10& =90 & 90:10& =9 \end{align} |
По-прежнему не нужны знаки "$$", каждая строка уравнений автоматически получает номер, который можно подавить, написав \notag перед "\\", и по-прежнему есть вариант со звездочкой align* , который формулы не нумерует.
При грамотном применении окружения align в строке должно стоять нечетное число знаков "&". Именно, если у нас




Полезное применение align возникает, когда идущие подряд выключные формулы содержат текстовые комментарии. Желательно, чтобы эти комментарии были выровнены. Вот как можно этого добиться с помощью align:
 | \begin{align*} 3\cdot 5+7\cdot 5&=(3+7) \cdot5 &&\text{(ясно)}\\ &=50&&\text{(очевидно)} \end{align*} |
Не всегда удобно включать комментарии к выкладкам прямо в формулы. Иногда хочется, чтобы какой-то из комментариев шел в отдельной строке. Команда \intertext позволяет сделать это так, чтобы выравнивание не нарушилось:
 | \begin{align*} 3\cdot 5+7\cdot 5&=(3+7) \cdot5 &&\text{(ясно)}\\ &=50&&\text{(очевидно),}\\ \intertext{откуда} 15+35 &=50 \end{align*} |
 | $$ \left\{ \begin{aligned} x^2+y^2&=7\\ x+y & = 3.\\ \end{aligned} \right. $$ |
Наконец, еще один тип многострочных выключных формул возникает, когда выражение в правой части равенства должно выглядеть по-разному в разных случаях.
На этот случай в пакете amsmath предусмотрено окружение cases. Продемонстрируем его работу сразу на примере:
 | $$ |x|=\begin{cases} x,&TeXt{если $x>0$;}\\ 0,&TeXt{если $x=0$;}\\ -x,&TeXt{если $x<0$.} \end{cases} $$ |
Теперь, когда вы ознакомились с возможностями набора многострочных формул с помощью пакета amsmath, расскажем и о том, что можно сделать в этом направлении без подключения дополнительных стилевых пакетов.
Системы уравнений можно набирать с помощью окружения array таким образом:
 | $$ \left\{ \begin{array}{rcl} x^2+y^2&=&7\\ x+y & = &3.\\ \end{array} \right. $$ |
Можно заметить, что пробелы (отбивки) до и после знака равенства получаются больше, чем это допускается типографскими правилами (и чем получается при использовании окружения aligned из пакета amsmath). К сожалению, бороться с этим трудно; проще раздобыть комплект, в который входит пакет amsmath .
Если необходимо, чтобы отдельные уравнения в системе были пронумерованы, можно воспользоваться окружением eqnarray . Оно работает так же, как окружение array с преамбулой rcl в вышеприведенном примере, но при этом у каждого уравнения автоматически печатается его номер (подобно тому, как автоматически печатается номер у выключной формулы, созданной с помощью окружения equation —. Если пометить какое-либо уравнение с помощью команды \label, то в дальнейшем можно на него ссылаться с помощью команды \ref или \pageref.
 | \begin{eqnarray} 2\times3&=&6\\ 2+3&=&5\label{silly} \end{eqnarray} На с.~\pageref{silly} приведено глупое уравнение~\ref{silly} |
В этом примере символ "~ "между "с."\ и \pageref поставлен, чтобы слово "с."\ и номер страницы не попали на разные строки ; для аналогичных целей мы использовали этот символ и вторично.
При использовании окружения eqnarray не надо писать знаки "$$" (подобно тому, как не надо их писать при пользовании окружением equation).
Если вы хотите нумеровать не все уравнения, надо уравнения, которые вы нумеровать не будете, пометить командой \nonumber (непосредственно перед "\\"):
 | \begin{eqnarray} \int_{-\infty}^\infty e^{-x^2}dx & = & \sqrt{\pi}\nonumber\\ \sqrt{576} & = & 24 \end{eqnarray} |
Окружение array можно использовать не только в выключных, но и во внутритекстовых формулах, хотя результат при этом обычно выглядит некрасиво. Окружения eqnarray и eqnarray* создают только выключные формулы.
Чтобы разбить выключную формулу на несколько выровненных частей, также можно воспользоваться окружением eqnarray или eqnarray*:
 | \begin{eqnarray*} x^{20}&=&(x-1)^{20}+ 20(x-1)^{19}+\ldots+\\ &&{}+20(x-1)+1 \end{eqnarray*} |

Набор коммутативных диаграмм
Чтобы набирать в LaTeX'е "коммутативные диаграммы", необходимо подключить стилевой пакет amscd. Пусть это сделано. Тогда коммутативная диаграмма оформляется в виде окружения CD. Читателю, знакомому с AMS-TeX'ом, дальнейшее можно объяснить одной фразой: между "\begin{CD}" и "\end{CD}" надо поместить в точности тот же текст, что в MS-TeX'е пишут в аналогичном случае между \CD и \endCD . Для всех остальных удобнее пояснить правила набора коммутативных диаграмм на примере. Рассмотрим следующую диаграмму:

При подключенном пакете amscd она набирается следующим образом:
$$ \begin{CD} 0 @”> E' @>f” E @>g” E'' @”> 0\\ @. @VVpV @VVqV @VVrV @.\\ 0 @”> F' @>f” F @>g” F'' @”> 0 \end{CD} $$Первая строка в этой записи соответствует верхней строке диаграммы. Стрелка, направленная слева направо, задается конструкцией "@”>" (а стрелка справа налево — конструкцией "@“<"); если над стрелкой надо поставить какую-то надпись (например, просто букву), то нужно ее разместить между первым и вторым знаками неравенства; чтобы надпись получилась под стрелкой, надо ее разместить между вторым и третьим знаками неравенства.
Вторая строка задает вертикальные стрелки. Конструкция "@VVV" задает стрелку, направленную вниз; если справа от стрелки нужна надпись, то ее надо разместить между второй и третьей буквами {V} (чтобы надпись оказалась слева от стрелки, она должна быть, естественно, между первой и второй буквами V). Вертикальная стрелка, направленная вверх, задается конструкцией "@AAA" (буква A — максимальное приближение к устремленной вверх стрелке); справа и слева от нее также можно сделать надпись (аналогичным образом).
Конструкция "@." задает "пустую" стрелку (в нашем случае — между двумя нулями); она необходима, чтобы LaTeX не сбился со счета, выясняя, в какие колонки ставить вертикальные стрелки.
Опишем работу окружения CD более аккуратно. Каждую коммутативную диаграмму окружение CD рассматривает как таблицу, состоящую из перемежающихся "горизонтальных" и " вертикальных" строк.
Каждая "горизонтальная" строка состоит из формул, перемежающихся горизонтальными стрелками. Во всех горизонтальных строках должно быть одинаковое количество формул. Если некоторые из мест, предназначенных для формул, должны остаться пустыми, то на этом месте надо оставить пробел или, если вам так приятнее, написать "{}". Между каждой парой формул должна быть стрелка. Если какие-то из этих стрелок не нужны, на их месте надо поставить "@." (" пустую" стрелку).
Каждая "вертикальная" строка состоит из вертикальных стрелок. Их должно быть столько же, сколько формул в любой из горизонтальных строк. Если какие-то из вертикальных стрелок не нужны, на их месте надо поставить "@." (пустую стрелку).
Если надпись при стрелке, направленной вниз (и задаваемой, стало быть, конструкцией "@VVV"), сама содержит букву V, то нужно ее (надпись) взять в фигурные скобки — иначе TeX не сможет понять, какая из букв V относится к надписи, а какая — к обозначению стрелки. Аналогичные меры надо принять, если надпись при стрелке, направленной вверх, содержит букву A (а также, естественно, если надпись при горизонтальной стрелке содержит знак ">" или "<", хотя ввиду математического смысла таких надписей последнее менее вероятно).
Наряду со стрелками, в коммутативных диаграммах встречаются горизонтальные и вертикальные "растянутые знаки равенства":
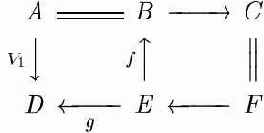
$$ \begin{CD} A @= B @”> C \\ @V{V_1}VV @AfAA @| \\ D @“g< E @“< F \end{CD} $$ Как видно из этого примера, такие знаки задаются конструкциями "@=" (горизонтальный) и "@|" (вертикальный). Обратите также внимание, как мы защитили фигурными скобками символ {V} в надписи к левой вертикальной стрелке.
Конструкция "\pretend" \ldots\ "\haswidth" системы AMSTeX в LaTeX'е не поддерживается.
Математики знают, что в коммутативных диаграммах могут встречаться не только горизонтальные и вертикальные стрелки: бывают и наклонные, и изогнутые, и пунктирные\...\ Возможностей пакета amscd для печати таких стрелок недостаточно; если вам нужны такие более сложные диаграммы, стоит воспользоваться стилевым пакетом Xy-pic (см.
приложение Д).
В "чистом" (без подключения стилевых пакетов) LaTeX' е набор диаграмм не предусмотрен. На самый крайний случай, если нет ни amscd, ни Xy-pic'а, можно сделать так:
$$ \begin{array}{ccccccccc} 0&\longrightarrow & E' & \stackrel{f}{\longrightarrow}& E & \stackrel{g}{\longrightarrow} & E'' & \longrightarrow & 0\\ &&\downarrow\lefteqn{p}&&\downarrow \lefteqn{q}&&\downarrow\lefteqn{r}\\ 0&\longrightarrow & F' & \stackrel{f}{\longrightarrow}& F & \stackrel{g}{\longrightarrow} & F'' & \longrightarrow & 0 \end{array} $$ В результате получится почти такая же диаграмма, как в нашем первом примере (правда, буквы при вертикальных стрелках будут крупнее букв при горизонтальных, поскольку команда \stackrel уменьшает буквы). Единственное, что тут нуждается в пояснении, — команды \lefteqn. Они нужны для того, чтобы вертикальные стрелки с надписями были правильно центрированы. Если эти \lefteqn'ы опустить (и писать p вместо \lefteqn{p} и т.п.), то вертикальные стрелки с подписями окажутся не по центру, а сдвинутыми влево.
Для интересующихся объясним, в чем тут дело. В процессе верстки текста TeX учитывает, сколько места занимает тот или иной фрагмент формулы. В TeX'е предусмотрены специальные команды, позволяющие фальсифицировать эти данные. В частности, команда \lefteqn печатает формулу, являющуюся ее аргументом, но при этом сообщает TeX'у, что по горизонтали эта формула не занимает места вообще. Стало быть, с точки зрения TeX'а ширина элемента, стоящего во второй строке нашей таблицы, определяется только шириной стрелки, и при центрировании текст располагается так, чтобы именно стрелка была на равном расстоянии от краев, сколь бы длинна на самом деле ни была формула, стоящая в \lefteqn. Создатель TeX'а Дональд Кнут назвал такого рода приемы работы с TeX'ом "грязными трюками" (dirty tricks). Впрочем, при написании TeX'овских макропакетов используются трюки и похлеще.
Набор матриц
Сначала мы объясним, как набирать матрицы при подключенном пакете amsmath (что во всех отношениях лучше и удобнее), а в конце этого раздела расскажем, для полноты картины, о тех средствах набора матриц, которые доступны в " чистом" LaTeX'е (без подключения дополнительных стилевых пакетов).
Итак, предположим, что пакет amsmath подключен. Тогда для набора матриц, заключенных в круглые скобки, стоит воспользоваться окружением pmatrix. Вот как оно работает:
 | $$ \begin{pmatrix} a_{11}-\lambda & a_{12}&a_{13}\\ a_{21}& a_{22}-\lambda &a_{23}\\ a_{31}& a_{32}&a_{33}-\lambda\\ \end{pmatrix} $$ |
Строки матрицы разделяются с помощью команды "\\" в матрицах (последнюю строку заканчивать командой "\\" не надо), а элементы внутри одной строки, относящиеся к разным столбцам, отделяются друг от друга с помощью символа "&". Текст, соответствующий на печати одной строке матрицы, не обязан укладываться в одну строку TeX'овского файла; в одной строке TeX'овского файла можно поместить текст, соответствующий на печати нескольким строкам матрицы. Короче говоря, в окружении matrix также действует TeX'овский принцип" конец строки равносилен пробелу".
Прямоугольные таблицы из формул бывают заключены не только в круглые скобки; соответственно, определены окружения bmatrix, vmatrix и Vmatrix, отличающиеся от pmatrix только тем, что вместо круглых скобок таблица заключена соответственно в квадратные скобки



Если вам нужны матрицы с более чем десятью столбцами, нужно изменить максимальное количество столбцов, написав в преамбуле что-нибудь вроде следующего:
\setcounter{MaxMatrixCols}{20}(после этого максимальное число столбцов в матрице станет равно двадцати; на TeX'ническом языке это действие называется " присваивание нового значения счетчику MaxMatrixCols" см.
лекцию 7 ).
Можно также дать эту команду не в преамбуле, а в начале той выключной формулы, в которую входит ваша матрица; тогда разрешение увеличить число столбцов будет действительно только для матриц, входящих в эту выключную формулу.
Вот как можно набрать с помощью окружения matrix треугольник Паскаля:

Исходный текст для него выглядит так:
$$ \setcounter{MaxMatrixCols}{20} \begin{matrix} &&&& 1 && 1\\ &&& 1 && 2 && 1\\ && 1 && 3 && 3 && 1\\ && 1 && 4 && 6 && 4 && 1\\ 1 && 5 && 10 && 10 && 5 && 1 \end{matrix} $$ (заметим кстати, что в этом примере пустые элементы таблицы в конце строки опущены, так что число символов "&" в разных строках таблицы разное). Если бы мы не увеличивали MaxMatrixCols, то последняя строка вызвала бы сообщение об ошибке.
Чтобы получить в матрице горизонтальный ряд точек, простирающийся на несколько столбцов, используется команда \hdotsfor; ее обязательный аргумент — количество столбцов, занятых точками. В приведенном ниже примере обратите внимание на расстановку знаков "&" в строках, содержащих \hdotsfor:
 | $$ \begin{vmatrix} 0 & 0&\hdotsfor{2} &a_1\\ 1 & 0&\hdotsfor{2} &a_2\\ \hdotsfor{5}\\ \hdotsfor{2} &1 &0 &a_{n-1}\\ 0 & \hdotsfor{2} &1 &a_n \end{vmatrix} $$ |
Наряду с горизонтальными рядами точек, в матрицах приходится использовать вертикальные и диагональные многоточия. Для их набора используются команды \vdots и \ddots:
 | $$ \begin{pmatrix} a_{11}& a_{12} &\ldots & a_{1n}\\ a_{21}& a_{22} &\ldots & a_{2n}\\ \vdots& \vdots &\ddots & \vdots\\ a_{n1}& a_{n2} &\ldots & a_{nn} \end{pmatrix} $$ |
Наряду с матрицами, используемыми в выключных формулах, иногда приходится поместить небольшую матрицу и в формулу внутритекстовую. Естественно, и размеры символов, и интервалы между ними в такой матрице должны быть поскромнее. Для таких целей предназначено окружение smallmatrix (оно также становится доступным при подключении пакета amsmath). Вот пример его использования:
 | $[X,Y]=\bigl(\begin{smallmatrix}1 & 0\\0 & -1\end{smallmatrix}\bigr)$ |
Теперь, как мы и обещали, сообщим, какие возможности для набора матриц остаются, если не подключать дополнительных пакетов. В этом случае необходимо пользоваться LaTeX'овским окружением array. Вот как получить этими средствами пример со 73:
 | $$ \left(\begin{array}{ccc} a_{11}-\lambda & a_{12}&a_{13}\\ a_{21}& a_{22}-\lambda &a_{23}\\ a_{31}& a_{32}&a_{33}-\lambda \end{array}\right) $$ |
Скобки вокруг матрицы, набираемой с помощью окружения \array, всегда надо задавать самостоятельно.После \begin{array}, открывающего окружение, должна следовать (в фигурных скобках, поскольку это аргумент окружения array) так называемая преамбула матрицы, описывающая, сколько и каких столбцов должно быть в матрице. В нашем случае преамбула представляет собой три буквы ccc. Это значит, что в матрице 3 столбца (по букве на столбец), и что содержимое каждого из этих столбцов должно быть расположено по центру столбца c — от слова "centered". (Кроме c, в преамбуле может стоять буква l, означающая, что соответствующий столбец будет выровнен по левому краю (left), или r, означающая, что столбец будет выровнен по правому краю (right).)В остальном синтаксис такой же, как для окружения pmatrix и его аналогов. Команды \ldots, \vdots и \ddots по-прежнему можно использовать, а вот \hdotsfor — увы, нет.Аналога MaxMatrixCols для окружения array также нет (поскольку преамбула и так определяет точное число столбцов). Окружение smallmatrix в "чистом" LaTeX'е (без подключения дополнительных пакетов) также не предусмотрено.
Надстрочные знаки
Часто требуется поставить дополнительный значок над буквой или фрагментом формулы: черточку, "крышку", и т.п. В TeX'е для этих целей есть специальные команды.
Во-первых, можно поставить горизонтальную черту над любым фрагментом формулы с помощью команды \overline, как в следующем примере:
 | Часто используется обозначение $$ \overline{a_na_{n-1}\ldots a_1a_0}=10^na_n+\ldots+a_0. $$ Особенно часто так пишут в научно-популярных книгах. |
Для постановки других значков над буквами в формулах предусмотрены команды, перечисленные в следующей таблице, в которой, для примера, эти значки ставятся над буквой

| \hat a |  |
| \check a |  |
| \tilde a |  |
| \acute a |  |
| \grave a |  |
| \dot a |  |
| \ddot a |  |
| \breve a |  |
| \bar a |  |
| \vec a |  |
Между прочим, команда \bar ставит не совсем такую же черточку, как \overline.
Если поставить значок над буквой




 | Писать $\tilde i$ некрасиво; лучше писать так: $\tilde\imath$. |
Надстрочные знаки, перечисленные в таблице, можно ставить только над одиночными буквами: если сказать "\hat{a+b}", то получится некрасивая формула

 | Тождество $\widehat{f*g}=\hat f\cdot\hat g$ означает, что преобразование Фурье переводит свертку в произведение. |
Аналогичным образом можно поставить "волну" над фрагментом формулы с помощью команды \widetilde. В отличие от горизонтальной черты, генерируемой командой \overline, знаки, генерируемые командами \widehat и \widetilde, не могут быть сколь угодно широкими (максимально возможная ширина — в примере выше).
Кроме того, существует команда \overrightarrow, предназначенная для постановки стрелки над формулой:
 | Рассмотрим вектор $\overrightarrow{AB}$. |
Аналогичная ей команда \overleftarrow ставит над формулой стрелку, направленную влево, а не вправо.
Остальные команды для постановки акцентов в формулах не имеют " широких" вариантов.
Формулы типа \hat{\hat A}, в которых акцент ставится над буквой, уже имеющей акцент, могут выглядеть неудачно. Если вам нужны такие "двойные акценты", подключите пакет \amsmath и пользуйтесь командами \Hat, \Check, \Tilde, \Acute, \Grave, \Dot, \Ddot, \Breve, \Bar и \Vec:
 | Правильно $\Hat{\Hat Z}$, а не $\hat{\hat Z}$. |
Впрочем, в последних версиях пакета amsmath команды типа \hat исправлены и действуют так же, как их аналоги с большой буквы.
Отметим, что TeX позволяет ставить надстрочные знаки над буквами не только в математической формуле, но и в обычном тексте (в этом случае такие знаки обычно называют "диакритическими"), но команды для постановки этих знаков совершенно другие. Об этом подробно в лекции 4.
Нумерация формул
В математических текстах обычно приходится для удобства ссылок нумеровать формулы; LaTeX позволяет организовать эту нумерацию таким образом, чтобы номера формул и ссылки на них генерировались автоматически . Нумеровать таким образом можно только выключные формулы. Делается это так.
Выключная формула, которую вы нумеруете, должна быть оформлена как окружение equation (знаков "$$" быть не должно!). Каждая такая формула на печати автоматически получит номер. Чтобы на него можно было ссылаться, надо формулу пометить: в любом месте между \begin{equation} и \end{equation} поставить команду \label, и после этого команда \ref будет генерировать номер формулы ; напомним, что может понадобиться повторный запуск LaTeX'a). Поясним сказанное примером:
 | Как известно, \begin{equation} \label{trivial} 7\times9=63. \end{equation} ......................... Из формулы~(\ref {trivial}) следует, что $63/9=7$. |
Знак "~" мы поставили, чтобы номер формулы и слово " формулы" не попали на разные строки . Обратите внимание, что скобки вокруг номера формулы, сгенерированного командой \ref, автоматически не ставятся. Если вы подключили пакет \amsmath, то можете воспользоваться командой \eqref, единственным отличием которой от \ref является то, что она автоматически ставит скобки вокруг номера формулы.
Можно также использовать команду \pageref вместо \ref — тогда на печати получится не номер формулы, а номер страницы, на которую попала эта формула.
То, как именно выглядит на печати номер формулы, зависит от класса документа : например, в классе Tarticle (статья) формулы имеют сплошную нумерацию, а в классе book(книга) нумерация формул начинается заново в каждой лекции, и номер, скажем, формулы 5 из главы 3, генерируемый окружением equation, имеет вид (3.5). В лекции, посвященной модификации стандартных классов, мы расскажем, как можно самостоятельно менять вид номеров формул.
Кроме того, вы можете вообще не пользоваться автоматической генерацией номеров формул, а ставить их вручную.
Чтобы номер выглядел при этом красиво, удобно воспользоваться TeX'овской командой \eqno. Следующий пример показывает, как это делать:
 | Простое тождество $$ 7\times9=63\eqno (3.2) $$ известно каждому школьнику. |
Никаких автоматических ссылок на формулу, генерируемую командой \eqno или \leqno, TeX не создает, и в этом случае за корректность ссылок отвечаете только вы.
Одно над другим
В этом разделе речь пойдет о тех случаях, когда в формуле необходимо поместить один символ над другим. В разд."Операции с пределами и без" уже шла речь о частном случае этой проблемы: постановке " пределов" у знака суммы, интеграла или чего-нибудь еще в этом роде. Сейчас мы рассмотрим общий случай.
Операции, отношения и просто значки
Начнем с греческих букв. Имя команды, задающей строчную греческую букву, совпадает с английским названием этой буквы (например, буква


 | \alpha |
 | \beta |
 | \gamma |
 | \delta |
 | \epsilon |
 | \varepsilon |
 | \zeta |
 | \eta |
 | \theta |
 | \vartheta |
 | \iota |
 | \kappa |
 | \lambda |
 | \mu |
 | \nu |
 | \xi |
 | \pi |
 | \varpi |
 | \rho |
 | \varrho |
 | \sigma |
 | \varsigma |
 | \tau |
 | \upsilon |
 | \phi |
 | \varphi |
 | \chi |
 | \psi |
 | \omega |
Имя команды, задающей прописную греческую букву, пишется с прописной буквы (например, буква



 | \Gamma |
 | \Delta |
 | \Theta |
 | \Lambda |
 | \Xi |
 | \Pi |
 | \Sigma |
 | \Upsilon |
 | \Phi |
 | \Psi |
 | \Omega |
Читатель мог заметить, что прописные греческие буквы печатаются, в отличие от строчных, прямым шрифтом. Если вам нужны наклонные прописные греческие буквы (вроде

Следующая серия символов — символы, рассматриваемые TeX'ом как символы бинарных операций (наподобие знаков сложения, умножения и т.п.); TeX оставляет в формуле небольшие пробелы по обе стороны этих знаков, кроме случаев, когда есть основания считать, что эти знаки используются не для обозначения операций, а для других целей (если, например, стоят два плюса подряд, то дополнительного пробела между ними не будет). Итак, вот список символов бинарных операций:
 | + |
 | - |
 | * |
 | \pm |
 | \mp |
 | \times |
 | \div |
 | \setminus |
 | \cdot |
 | \circ |
 | \bullet |
 | \cap |
 | \cup |
 | \uplus |
 | \sqcap |
 | \sqcup |
 | \vee |
 | \wedge |
 | \oplus |
 | \ominus |
 | \otimes |
 | \odot |
 | \oslash |
 | \triangleleft |
 | \triangleright |
 | \amalg |
 | \diamond |
 | \wr |
 | \star |
 | \dagger |
 | \ddagger |
 | \bigtriangleup |
 | \bigcirc |
 | \bigtriangledown |
p> Обозначения для многих из выписанных знаков длинны и сложны. С этим неудобством борются следующим образом: если в вашем тексте часто встречается какое-то длинное обозначение для математического символа, имеет смысл определить для этого символа свою более удобную команду (например, btu вместо bigtriangleup). Как это сделать, рассказано в начале лекции 7; вы можете прочитать это уже сейчас.
В следующей таблице мы собрали символы "бинарных отношений". Вокруг них TeX также оставляет дополнительные пробелы (не такие, как вокруг символов бинарных операций). Вообще говоря, нет смысла много задумываться об этих пробелах, поскольку TeX оформляет математические формулы в достаточно разумном стиле; о тех случаях, когда размер пробелов в математических формулах приходится корректировать вручную, речь пойдет дальше в этой лекции.
 | < |
 | > |
 | = |
 | : |
 | \le |
 | \ge |
 | \ne |
 | \sim |
 | \simeq |
 | \approx |
 | \cong |
 | \equiv |
 | \ll |
 | \gg |
 | \doteq |
 | \parallel |
 | \perp |
 | \in |
 | \notin |
 | \ni |
 | \subset |
 | \subseteq |
 | \supset |
 | \supseteq |
 | \succ |
 | \prec |
 | \succeq |
 | \preceq |
 | \asymp |
 | \sqsubseteq |
 | \sqsupseteq |
 | \models |
 | \vdash |
 | \dashv |
 | \smile |
 | \frown |
 | \mid |
 | \bowtie |
 | \propto |
 | $M=\{\,x\in A\mid x>0\,\}$ |
Стоит еще отметить, что при записи отображений нужно использовать не двоеточие, а команду \colon:
 | $f\colon X\to Y$ |
Если вы подключите стилевой пакет latexsym, то вам, кроме того, будут доступны следующие семь символов:
 | \lhd |
 | \unlhd |
 | \rhd |
 | \unrhd |
 | \sqsubset |
 | \sqsupset |
 | \Join |
p> В следующей таблице собраны стрелки различных видов.
 | \to |
 | \longrightarrow |
 | \Rightarrow |
 | \Longrightarrow |
 | \hookrightarrow |
 | \mapsto |
 | \longmapsto |
 | \leadsto |
 | \gets |
 | \longleftarrow |
 | \Leftarrow |
 | \Longleftarrow |
 | \hookleftarrow |
 | \leftrightarrow |
 | \longleftrightarrow |
 | \Leftrightarrow |
 | \Longleftrightarrow |
 | \uparrow |
 | \Uparrow |
 | \downarrow |
 | \Downarrow |
 | \updownarrow |
 | \Updownarrow |
 | \nearrow |
 | \searrow |
 | \swarrow |
 | \nwarrow |
 | \leftharpoondown |
 | \leftharpoonup |
 | \rightharpoonup |
 | \rightharpoondown |
 | \rightleftharpoons |

Из привычных российскому читателю символов в вышеприведенных таблицах нет знаков









Операции с пределами и без
В следующей таблице собраны названия функций — команды для воспроизведения названий математических операций наподобие


 | \log |
 | \lg |
 | \ln |
 | \arg |
 | \ker |
 | \dim |
 | \hom |
 | \deg |
 | \exp |
 | \sin |
 | \arcsin |
 | \cos |
 | \arccos |
 | \tan |
 | \arctan |
 | \cot |
 | \sec |
 | \csc |
 | \sinh |
 | \cosh |
 | \tanh |
 | \coth |
В этой таблице обозначения




В первом аргументе команды \DeclareMathOperator ставится придуманное вами имя команды (незанятое, естественно), во втором — то, что вы хотите получить на печати. Содержимое второго аргумента будет обработано, как математическая формула, но при этом символы - (дефис), * и ' будут иметь такое же значение, как в обычном тексте (это удобно, если вы хотите, чтобы имя вашего нового оператора включало тот же дефис). Разумеется, \DeclareMathOperator должно следовать в преамбуле документа после \usepackage{amsmath}.
Если не подключать amsmath, то собственную функцию, например tangens, определить также можно. Для этого достаточно написать в преамбуле документа \newcommand{\tg}{\mathop{\mathrm{tg}}\nolimits} После этого команда \tg будет создавать в математической формуле запись

В частности, так приходится делать, чтобы определить команды \Re и \Im для обозначения вещественной и мнимой части комплексного числа; в LaTeX'е такие команды есть, но на печати они дают не




При этом, поскольку обозначения \Re и \ Im уже заняты, приходится говорить \renewcommand вместо \newcommand:
\renewcommand{\Im}{\mathop{\mathrm{Im}}\nolimits} Даже при подключенном пакете \amsmath команда \DeclareMathOperator в этом месте не сработает, т.к. уже существующие команды она не переопределяет.
Описанный выше способ определения команд для функций является частным случаем существующей в LaTeX'е конструкции для (пере)определения новых команд (см. лекцию 7).
Еще один символ, который принято набирать прямым шрифтом, — это символ


 | Легко видеть, что $23^{1993}\equiv 1\pmod{11}$ |

Если подключить пакет amsmath , то станут доступны команды \mod и \pod, обозначающие то же понятие, что \mod, другими способами:
  |
$a^{p-1}\equiv 1\mod p$ $a^{p-1}\equiv 1\pod p$ |

 | $f_*(x)=f(x)\bmod G$ |
Теперь обсудим, как можно было бы получить, скажем, формулу


 | Тот факт, что $\sum_{i=1}^n (2n-1)=n^2$ следует из формулы для суммы арифметической прогрессии. |
ниже). Вот список операций, ведущих себя так же, как \sum:
 | \sum |
 | \prod |
 | \bigcup |
 | \bigcap |
 | \coprod |
 | \bigoplus |
 | \bigotimes |
 | \bigodot |
 | \bigvee |
 | \bigwedge |
 | \biguplus |
 | \bigsqcup |
 | \lim |
 | \limsup |
 | \liminf |
 | \max |
 | \min |
 | \sup |
 | \inf |
 | \det |
 | \Pr |
 | \gcd |
 | \varlimsup |
 | \varliminf |
 | \injlim |
 | \projlim |
 | \varinjlim |
 | \varprojlim |
  |
$\varlimsup_{n\to\infty} a_n=\inf_n\sup_{m\ge n}a_m$ $\mathcal F_x= \varinjlim_{U\ni x}\mathcal F(U)$ |
Кроме того, пакет amsmath предоставляет возможность определить и собственную команду "с пределами". Для этого надо воспользоваться командой \DeclareMathOperator*; синтаксис этой команды такой же, как у команды \DeclareMathOperator , но при "операторе", определенном такой командой, " пределы" будут ставиться так же, как при

Еще одна "математическая операция", для которой требуются " пределы", — это интеграл. В LaTeX'е есть команды \int для обычного знака интеграла


При этом, для экономии места, пределы интегрирования помещаются не сверху и снизу от знаков интеграла, а по бокам (даже и в выключных формулах):
 | $$ \int_0^1x^2 dx=1/3 $$ |
 | $$ \int\limits_0^1 x^2 dx=1/3 $$ |
Если, с другой стороны, надо, чтобы в выключной формуле " пределы" у какого-либо оператора стояли не над и под знаком оператора, а сбоку, то после команды для знака оператора надо записать команду \nolimits, а уже после нее — обозначения для "пределов"
 | $$ \prod\nolimits_{i=1}^ni=n! $$ |
Перечеркнутые символы
Чтобы получить в математической формуле изображение перечеркнутого символа, надо перед командой, генерирующей этот символ, поставить команду \not. Пример:
 | Множество $\{x\mid x\not\ni x\}$ существовать не может. В этом состоит парадокс Рассела. |
Кстати, для получения знака

Переносы в формулах
При необходимости TeX может перенести часть внутритекстовой формулы на другую строчку. Такие переносы возможны после знаков "бинарных отношений", наподобие знака равенства1) или "бинарных операций", наподобие знаков сложения или умножения , причем последний знак в строке, вопреки российской традиции, не дублируется в начале следующей. Чтобы избежать этих переносов, можно воспользоваться тем обстоятельством, что TeX не разрывает при переносе часть формулы, заключенную в фигурные скобки. В частности, можно заключить в фигурные скобки всю формулу, в которой произошел нежелательный перенос, от открывающего ее знака доллара до закрывающего: после этого можно быть уверенным, что переноса этой формулы ни при каких обстоятельствах не произойдет.
Вышеописанный способ борьбы с неудачными переносами в формулах имеет один недостаток: при этом затрудняется верстка абзацев и возрастает вероятность появления неприятных сообщений "Overfull \hbox"(см. разд."Абзацы" лекция 3 ).
Более гибкий способ борьбы с переносами в формулах — записать в преамбуле файла строку
\binoppenalty=10000"и/или строку
relpenalty=10000Первая из этих строк запретит все разрывы строк после знаков бинарных операций, а вторая — после знаков бинарных отношений, и при этом помех верстке абзаца будет меньше, чем при заключении всей формулы в фигурные скобки.
Для любознательных поясним, что \binoppenalty и \relpenalty — параметры (TeX'овские), значением которых может быть целое число . Эти параметры определяют степень нежелательности разрыва строки после символов бинарной операции и бинарного отношения соответственно (чем больше значение соответствующего параметра, тем менее желателен разрыв строки). По умолчанию значение \binoppenalty равно


При заключении всей формулы в фигурные скобки верстка абзацев затрудняется, поскольку TeX лишается возможности варьировать в ней интервалы между символами для выравнивания строк (см.
разд."Абзацы"лекция 3 ).
Наконец, существует способ дублировать знаки операций, который мы приведем безо всяких пояснений. Включив
\newcommand*{\hm}[1]{#1\nobreak\discretionary{}% {\hbox{\mathsurround=0pt #1}}{}}в преамбулу, можно написать $a\hm+b\hm+c\hm+d$, при этом в формуле


Выключные формулы, в отличие от внутритекстовых, TeX никогда не переносит. Если выключная формула не помещается в строку, то при трансляции вы получите сообщение "Overfull \hbox" (в разд. "Абзацы"лекция 3 подробно рассказано, в каких еще ситуациях выдается такое сообщение), и вам придется разбить формулу на строки вручную. Как это делать, мы объясним в разд. "Многострочные и выключные формулы".
Пробелы вручную
Бывают случаи, когда промежутки между символами в формулах, выбранные TeX'ом автоматически, выглядят неудачно. В этом случае в формулу можно включить команды, задающие промежутки в явном виде. Вот основные из них:

Команда \! из этой таблицы уменьшает промежуток на столько же, на сколько команда \, его увеличивает.
В следующем примере собраны типичные случаи, когда в этих командах возникает нужда.
 | $$ Пробелы надо корректировать в таких формулах, как $\int f(x)\,dx$, $\int\!\!\int f\,dx\,dy$ или $\sqrt{3}\,x$. $$ |
Команда \qquad полезна для отделения текста, входящего в формулу, от собственно формулы. Для этих же целей можно использовать команду \quad, делающую пробел размером {1em}. Вместо \int\!\!\int лучше, конечно, подключить пакет amsmath и сказать \iint.
Простейшие случаи
Для начала рассмотрим такие возможности расположения одной части формулы над другой:
Верхняя часть формулы расположена немного выше строки, нижняя — немного ниже (как в дроби, создаваемой командой \frac, но, возможно, без дробной черты).Нижняя часть формулы расположена вровень с остальным текстом, верхняя — над ним.Над или под фрагментом формулы проведена горизонтальная фигурная скобка, а над или под этой скобкой расположен другой фрагмент формулы.Разберем эти варианты последовательно.
Начнем с одного дополнения по поводу описанной в первой лекции команды \frac, задающей дроби. Если дробь, заданная с помощью команды \frac, встречается во внутритекстовой формуле, то ее числитель и знаменатель печатаются довольно мелким шрифтом, что не всегда приемлемо. Чтобы этого избежать, можно, подключив пакет amsmath, воспользоваться командой \dfrac: тогда шрифт будет более крупным. Если дробь во внутритекстовой формуле входит в показатель степени или индекс, то иногда имеет смысл задавать ее с помощью команды \tfrac (опять-таки чтобы шрифт был не слишком мелким; эта команда также доступна при подключении amsmath). Вот примеры:
 
 | $\frac23$ и $\dfrac23$ $2^{\frac35}$ и $2^{\tfrac35}$ |
Теперь о том, как расположить части формулы "так же, как в дроби ", но без дробной черты. Для этого есть два (к сожалению, взаимоисключающих) способа: с подключением пакета amsmath и без этого пакета.
Если у вас подключен пакет amsmath, можно добиться требуемого эффекта с помощью ограничителей и окружения smallmatrix:
 | Раньше вместо $\Gamma^k_{ij}$ писали $\left\{ \begin{smallmatrix}ij\\k \end{smallmatrix}\right\}$. |
Конечно, если таких формул у вас в тексте много, пользоваться столь длинными обозначениями немыслимо: нужно на базе smallmatrix разработать сокращенное обозначение (прочтите в лекции 7, как определять " макросы с параметрами").
Для наиболее часто встречающегося случая "биномиальных коэффициентов", когда ограничителями являются обычные круглые скобки, в пакете amsmath предусмотрена специальная команда \binom, работающая аналогично \frac:
 | $\binom{12}7=792$ |
p>У команды \binom есть также аналоги \dbinom и \tbinom, относящиеся к ней так же, как \dfrac и \tfrac относятся к \frac.
В пакете amsmath предусмотрена также конструкция " обобщенной дроби", предназначенная для создания команд, аналогичных \frac и \binom. По определению, обобщенная дробь — это фрагмент формулы, устроенный так: левый ограничитель, затем дробь (толщина дробной черты может быть произвольной, в том числе нулевой), затем правый ограничитель. Напомним, что ограничители — это скобки и им подобные символы, способные автоматически менять размер; в обобщенной дроби ограничители могут и отсутствовать (так что обычная дробь — действительно частный случай обобщенной). Для набора обобщенной дроби предусмотрена команда \genfrac с шестью аргументами. Чтобы понять, как она работает, посмотрим на пример:
 | Формула $\genfrac{(}{]}{1pt}{0}{x}{y-z}$ лишена всякого смысла. |
Если оставить третий аргумент пустым, написав просто "{}" вместо фигурных скобок, в которых записана толщина, то будет выбрана толщина дробной черты по умолчанию (она равна 0.4 пункта). Если оставить первый и второй аргумент пустыми, то ограничителей не будет (если, однако, левый ограничитель указан, то должен быть указан и правый). Например, "\dfrac{x}{y}" - это то же самое, что
\genfrac{}{}{}{0}{x}{y} В частности, наш пример с символом Кристоффеля можно записать как

Конечно, команда \ genfrac хороша не сама по себе, а как сырье для определения макросов, приспособленных к вашим конкретным нуждам.
Теперь о том, как быть, если вы не подключаете пакет amsmath. В этом случае удобно воспользоваться TeX'овской командой \atop:
 | Раньше вместо $\Gamma^k_{ij}$ писали $\left\{ij\atop k\right\}$. |
Для биномиальных коэффициентов есть TeX'овская команда \choose\,
 | $$ {n\choose k}=\frac{n!}{k!(n-k)!} $$ |

Команда \atop определяет, что пойдет вверх, а что — вниз, по тем же правилам, что и \choose . В примере выше с \atop мы обошлись без фигурных скобок, поскольку в математической формуле их функцию исполняют также команды \left и \right .
При подключенном пакете amsmath командами \atop и \choose пользоваться нельзя.
Интересный случай использования дробей — так называемые " цепные дроби"

 | $$ \frac{7}{25}= \frac{1}{ 3+\frac{1}{ 1+\frac{1}{ 1+\frac{1}{3}}}} $$ |
 | $$ \frac{7}{25}= \cfrac{1}{ 3+\cfrac{1}{ 1+\cfrac{1}{ 1+\cfrac{1}{3}}}} $$ |
Еще один случай, когда надо напечатать две формулы одинакого размера одну под другой, встречается, когда выражение для индексов суммирования занимает несколько строчек.
В этом случае надо, подключив пакет amsmath, воспользоваться командой \substack:
 | $$ \sum_{\substack{i\in[0;n]\\ j\in[0;m]}} a_{ij} $$ |
Рассмотрим случай, когда нижняя часть формулы должна остаться на уровне строки. Чтобы добиться этого эффекта, используется LaTeX'овская команда \stackrel. У этой команды два аргумента: первый — то, что будет над строкой, второй — то, что останется в строке:
 | $A\stackrel{f}{\longrightarrow}B$ |
 | $$ A\xleftarrow[z]{f}B \xrightarrow{f+g-h}C $$ |

$$ \underbrace{1+3+5+7+ \ldots+(2n-1)}_{\mbox{$n$ слагаемых}}=n^2 $$ Если у вас подключен пакет amsmath, разумно воспользоваться командой \text вместо \mbox.
Горизонтальная фигурная скобка над фрагментом формулы генерируется командой \overbrace, надпись над ней оформляется как верхний индекс. В одной формуле могут присутствовать горизонтальные фигурные скобки как над, так и под фрагментом формулы:
 | $$ \overbrace{\underbrace{ a+b+\ldots+z }_{26}+1+ \ldots+10}^{36} $$ |
Размер символов в формулах
В большинстве случаев вам не приходится задумываться о том, какой размер будут иметь символы в формуле: TeX автоматически выбирает более мелкий шрифт для степеней, индексов, числителей и знаменателей дробей, созданных командой \frac, и т.п. Бывают, однако, случаи, когда в этот процесс автоматического выбора размера приходится вмешаться. Сейчас мы вкратце опишем, как TeX выбирает размеры символов в формулах и как можно на него при этом влиять.
При наборе формулы TeX в каждый момент руководствуется одним из следующих "стилей":
| displaystyle | " выключной" стиль |
| textstyle | " текстовый" стиль |
| scriptstyle | стиль для индексов |
| scriptscriptstyle | стиль для индексов к индексам. |
" Выключной" и "текстовый" стили используют одинаковые шрифты, но формулы в текстовом стиле выглядят чуть скромнее (например, в выключном стиле верхние индексы поднимаются повыше, а нижние опускаются пониже, чем в текстовом; в текстовом стиле " пределы" операций записываются не сверху, а сбоку —. В стиле для индексов используются более мелкие шрифты, чем в выключном или текстовом (а в стиле для индексов к индексам — еще более мелкие). Выбираются стили набора формул следующим образом: выключная формула начинает набираться в выключном стиле, внутритекстовая — в текстовом стиле; далее, если в момент действия какого-то из стилей встретится команда \frac (или \atop), то для набора числителя и знаменателя TeX переключается на следующий по порядку стиль из вышеприведенной таблицы; если в момент действия выключного или текстового стиля встретится верхний или нижний индекс (показатель степени мы также рассматриваем как верхний индекс — в математическое содержание формул TeX не вникает), то этот индекс начинает набираться стилем для индексов; если индекс встретится в момент действия стиля для индексов или индексов к индексам, то набираться он будет в стиле "индексы к индексам". Например, при наборе формулы





Стиля {scriptscriptscriptstyle} и дальнейших не предусмотрено, так что индексы третьего и более высоких порядков набираются теми же шрифтами, что и индексы второго порядка (расстраиваться по этому поводу не надо, поскольку эти шрифты и так мелкие).
Если вы хотите изменить стиль набора формулы, можно в явном виде указать его с помощью TeX'овской команды, имя которой совпадает с английским названием этого стиля (\displaystyle... \scriptscriptstyle)). Вот типичный пример, когда это может понадобиться. Предположим, в вашем тексте встречаются "цепные дроби". На стр.79 показано, какой неудачный результат выйдет, если набирать цепную дробь наивным образом. Теперь мы видим, что этот результат формально полностью согласуется с правилами TeX'а: вся формула, коль скоро она выключная, набирается в выключном стиле, стало быть числитель и первый из знаменателей будут уже в текстовом стиле, следующий знаменатель — как индексы, следующий — как индексы к индексам, и т.д. Если нет возможности воспользоваться командой \cfrac из пакета amsmath, то надо набирать так:
$$ \frac{7}{25}= \frac{1}{\displaystyle 3+\frac{1}{\displaystyle 1+\frac{1}{\displaystyle 1+\frac{1}{3}}}} $$

Разное
Мы уже перечислили почти все символы, используемые LaTeX'ом в математических формулах (кроме большого количества тех, доступ к которым открывается при подключении пакета amssymb — см. разд. "Символы из пакета amssymb "ниже. Остались скобки различных видов (им будет посвящен специальный разд. "Скобки переменного размера"), а также ряд значков (среди них есть и часто встречающиеся), не входящих ни в какой из разделов нашей классификации. Они собраны в следующей таблице.
 | \partial |
 | \triangle |
 | \angle |
 | \infty |
 | \forall |
 | \exists |
 | \emptyset |
 | \neg |
 | \aleph |
 | \prime |
 | \hbar |
 | \nabla |
 | \imath |
 | \jmath |
 | \ell |
 | \surd |
 | \flat |
 | \sharp |
 | \natural |
 | \top |
 | \bot |
 | \wp |
 | \Re |
 | \Im |
 | \backslash |
 | \| |
 | \spadesuit |
 | \clubsuit |
 | \diamondsuit |
 | \heartsuit |
 | \dag |
 | \S |
 | \copyright |
 | \ddag |
 | \P |
 | \pounds |
Последние шесть символов (от \dag до \pounds) можно использовать не только в формулах, но и в тексте.
Если подключить стилевой пакет latexsym, то будут также доступны следующие команды:
 | \mho |
 | \Box |
 | \Diamond |
Символ


Не следует смешивать команды \parallel и \|. На печати они дадут один и тот же значок

 | В школьных учебниках геометрии встречаются такие формулы, как $AB\parallel CD$. В университетских учебниках анализа часто пишут, что $\|A\|=\sup(|Ax|/|x|)$. |
Символы, обозначаемые командами \imath и \jmath, нужны для постановки дополнительных значков над буквами


Команды \nabla и \bigtriangledown задают разные символы, и их не надо путать. Обратите также внимание на символ, задаваемый командой \prime.
Это — тот самый штрих, который используется в качестве верхнего индекса, если после символа в формуле поставить знак "'" ; на самом деле записи "x'" и "x^" практически равносильны.
Приведем еще таблицу синонимов. В ней представлены математические символы, которые можно набирать двумя различными способами:
 | * или \ast |
 | \ne или \neq |
 | \le или \leq |
 | \ge или \geq |
 | [ или \lbrack |
 | ] или \rbrack |
 | \{ или \lbrace |
 | \} или \rbrace |
 | \to или \rightarrow |
 | \gets или \leftarrow |
 | \ni или \owns |
 | \wedge или \land |
 | \vee или \lor |
 | \neg или \lnot |
 | \Vert или \| |
Символы из пакета amssymb
Математических знаков в стандартном LaTeX'овском наборе очень много, но порой и их не хватает. Если вы подключите пакет amssymb, то сможете воспользоваться дополнительными математическими знаками, разработанными Американским математическим обществом (сокращенно AMS — American Mathematical Society). Этих знаков более полутора сотен; мы опять разобьем их на группы.
Начнем с бинарных операций. Стилевой пакет amssymb дает возможность воспользоваться такими символами, относящимися к этой категории:
 | \boxdot |
 | \centerdot |
 | \barwedge |
 | \Cap |
 | \leftthreetimes |
 | \intercal |
 | \circleddash |
 | \gtrdot |
 | \smallsetminus |
 | \boxplus |
 | \boxminus |
 | \doublebarwedge |
 | \rightthreetimes |
 | \circledcirc |
 | \divideontimes |
 | \ltimes |
 | \boxtimes |
 | \veebar |
 | \Cup |
 | \curlyvee |
 | \dotplus |
 | \circledast |
 | \lessdot |
 | \rtimes |
Следующим по очереди идет огромное количество бинарных отношений:
 | \rightleftharpoons |  | \leftrightharpoons |
 | \Vdash |  | \Vvdash |
 | \vDash |  | \upharpoonright |
 | \downharpoonright |  | \upharpoonleft |
 | \downharpoonleft |  | \Lsh |
 | \Rsh |  | \circeq |
 | \succsim |  | \gtrsim |
 | \gtrapprox |  | \multimap |
 | \therefore |  | \because |
 | \doteqdot |  | \triangleq |
 | \precsim |  | \lesssim |
 | \lessapprox |  | \eqslantless |
 | \eqslantgtr |  | \curlyeqprec |
 | \curlyeqsucc |  | \preccurlyeq |
 | \leqq |  | \leqslant |
 | \lessgtr |  | \risingdotseq |
 | \fallingdotseq |  | \succcurlyeq |
 | \geqq |  | \geqslant |
 | \gtrless |  | \sqsubset |
 | \sqsupset |  | \vartriangleright |
 | \vartriangleleft |  | \trianglerighteq |
 | \trianglelefteq |  | \between |
 | \blacktriangleright |  | \blacktriangleleft |
 | \vartriangle |  | \eqcirc |
 | \lesseqgtr |  | \gtreqless |
 | \lesseqqgtr |  | \gtreqqless |
 | \varpropto |  | \smallsmile |
 | \smallfrown |  | \Subset |
 | \Supset |  | \subseteqq |
 | \supseteqq |  | \bumpeq |
 | \Bumpeq |  | \lll |
 | \ggg |  | \pitchfork |
 | \backsim |  | \backsimeq |
 | \lvertneqq |  | \gvertneqq |
 | \lneqq |  | \gneqq |
 | \lneq |  | \gneq |
 | \precnsim |  | \succnsim |
 | \lnsim |  | \gnsim |
 | \precneqq |  | \succneqq |
 | \precnapprox |  | \succnapprox |
 | \lnapprox |  | \gnapprox |
 | \varsubsetneq |  | \varsupsetneq |
Несколько символов из этой таблицы нам уже знакомы: в первую очередь это знаки для нестрогих неравенств








Специальные команды предусмотрены для отрицаний отношений из предыдущей таблицы. В принципе "отрицание" (перечеркнутый символ) можно напечатать, поставив перед этим символом команду \not , но взаимное расположение черты и перечеркиваемого символа при этом не всегда удачно. Поэтому Американское математическое общество выделило для перечеркнутых символов специальные литеры (ради красоты приходится страдать ...). Итак:
 | \nleq |  | \ngtr |
 | \nleqslant |  | \nsucceq |
 | \nsupseteqq |  | \nsim |
 | \nparallel |  | \nshortparallel |
 | \nvDash |  | \ntrianglelefteq |
 | \nleftarrow |  | \nRightarrow |
 | \ngeq |  | \nprec |
 | \ngeqslant |  | \nleqq |
 | \ncong |  | \nsubseteq |
 | \nmid |  | \nvdash |
 | \nVDash |  | \ntriangleleft |
 | \nrightarrow |  | \nLeftrightarrow |
 | \nless |  | \nsucc |
 | \npreceq |  | \ngeqq |
 | \nsubseteqq |  | \nsupseteq |
 | \nshortmid |  | \nVdash |
 | \ntrianglerighteq |  | \ntriangleright |
 | \nLeftarrow |  | \nleftrightarrow |
 | \circlearrowright |  | \circlearrowleft |
 | \twoheadrightarrow |  | \twoheadleftarrow |
 | \leftleftarrows |  | \rightrightarrows |
 | \upuparrows |  | \downdownarrows |
 | \rightarrowtail |  | \leftarrowtail |
 | \rightsquigarrow |  | \leftrightsquigarrow |
 | \looparrowleft |  | \looparrowright |
 | \Rrightarrow |  | \Lleftarrow |
 | \nleftarrow |  | \nrightarrow |
 | \nLeftarrow |  | \nRightarrow |
 | \nLeftrightarrow |  | \nleftrightarrow |
 | \curvearrowleft |  | \curvearrowright |

В приведенной выше таблице присутствует команда \rightleftharpoons, входящая в основной набор LaTeX'а; ниже можно найти еще несколько аналогичных примеров. Такое дублирование — не прихоть TeXнологов из AMS: в базовом LaTeX'е символы, задаваемые этими дублирующимися командами, собирались из отдельных кусочков, вследствие чего они не меняли должным образом размеры при помещении в индексы. В пакете amssymb те же команды отсылают к специальным литерам, входящим в шрифты AMS, в результате чего символы


Теперь перечислим обыкновенные символы, доступ к которым открывается при подключении пакета amssymb:
 | \square |  | \blacksquare |
 | \lozenge |  | \blacklozenge |
 | \backprime |  | \bigstar |
 | \blacktriangledown |  | \blacktriangle |
 | \triangledown |  | \angle |
 | \measuredangle |  | \sphericalangle |
 | \circledS |  | \complement |
 | \diagup |  | \diagdown |
 | \varnothing |  | \nexists |
 | \Finv |  | \Game |
 | \mho |  | \eth |
 | \beth |  | \gimel |
 | \daleth |  | \digamma |
 | \varkappa |  | \Bbbk |
 | \hslash |  | \hbar |





Команды \yen, \checkmark, \circledR и \maltese можно использовать не только в формулах, но и в тексте (кстати, \yen — это обозначение для японской иены).
У некоторых из символов, определенных в пакете amsfonts, тоже есть синонимы. Вот их список:
 | \dasharrow или \dashrightarrow |
 | \Doteq или \doteqdot |
 | \Cup или \doublecup |
 | \Cap или \doublecap |
 | \lll или llless |
 | \ggg или gggtr |
 | \yen |  | \checkmark |
 | \circledR |  | \maltese |
 | \dasharrow |  | \dashleftarrow |
 | \sqsubset |  | \sqsupset |
 | \vartriangleleft |  | \vartriangleright |
 | \trianglelefteq |  | \trianglerighteq |
 | \square |  | \lozenge |
 | \rightsquigarrow |  | \rightleftharpoons |
Скобки переменного размера
Если заключенный в скобки фрагмент формулы занимает много места по вертикали (за счет дробей, степеней и тому подобного), то и сами скобки должны быть большего размера, чем обычные. В TeX'е на этот случай предусмотрен механизм автоматического выбора размера скобок. Пользуются им так.
В формуле


Если перед одной скобкой стоит \left, а перед другой скобкой стоит \right, то на печати размер этих скобок будет соответствовать максимальной высоте фрагмента формулы, заключенного между \left и \right.
Конструкция с \left и \right применима не только к круглым скобкам. В следующей таблице перечислены скобки и некоторые другие символы, которые с помощью \left и \right автоматически принимают нужный размер. TeXнический термин для таких символов — ограничители (по-английски delimiters).
 | ( |
 | ) |
 | [ |
 | ] |
 | { |
 | } |
 | \lfloor |
 | \lceil |
 | \rceil |
 | \langle |
 | \rangle |
 | | |
 | \| |
 | / |
 | \ |
Вместо \left\langle можно писать \left< , и аналогичным образом вместо \right\rangle можно писать \right> (однако же < нельзя писать вместо \langle!). Кроме знаков, перечисленных в этой таблице, менять свои размеры под действием \left и \right могут и вертикальные стрелки из таблицы.
Если подключить стилевой пакет amssymb, то станут доступны еще две пары ограничителей:
 | \ulcorner |
 | \urcorner |
 | \llcorner |
 | \lrcorner |
Вместе с каждой командой \left в формуле должна присутствовать соответствующая ей команда \right, в противном случае TeX выдаст сообщение об ошибке. Вместе с тем TeX вовсе не требует, чтобы "ограничители" (например, скобки) при командах \left и \right были расположены сколько-нибудь осмысленно с математической точки зрения: вы вполне можете написать что-нибудь вроде \left(...\right] , или даже, вопреки смыслу слов left и right,\left)...\right(- за правильность своих формул отвечаете только вы, и TeX тут вам не помощник.
Вместо "ограничителя" после команды \left или \ right можно поставить точку. На месте этой точки ничего не напечатается, а другой "ограничитель" будет необходимого размера. Вот два примера того, как можно использовать этот прием. Во-первых, таким способом можно создать косую дробную черту увеличенного размера (символ {/} также является "ограничителем"- см. ниже):
 | $$ M(f)=\left.\left( \int\limits_a^b f(x)\,dx \right) \right/(b-a) $$ |


 | $$ \int\limits_a^b\frac12 (1+x)^{-3/2}dx= \left.-\frac{1}{\sqrt{1+x}} \right|_a^b $$ |
Наконец, важный пример использования ограничителей без пары — использование их для набора систем уравнений, о чем пойдет речь в разд."Многострочные включные формулы".
До сих пор у нас речь шла только о том, что размеры ограничителей выбираются автоматически с помощью команд \left и \right; бывают, однако, ситуации, когда такой автоматический выбор размера приводит к неудовлетворительным результатам или даже вообще невозможен. Вот, например, ситуация, когда \left и \right не срабатывают:
 | $\left| |x+1|-|x-1|\right|$ |
А иногда бывает так, что автоматически получающиеся ограничители слишком велики. В следующем примере совсем не обязательно, чтобы скобки охватывали и пределы суммирования, что получается при использовании \left и \right:
 | $$ \left( \sum_{k=1}^n x^k \right)^2 $$ |
p> Во всех этих случаях имеет смысл указать размер ограничителя явно. Для этого предусмотрены TeX'овские команды \bigl, \Bigl, \biggl и \Biggl для левых ограничителей и \bigr, \Bigr, \biggr и \Biggr для правых ограничителей. Мы перечислили эти команды в порядке возрастания размера создаваемого ими ограничителя. В частности, для модулей можно было бы написать так:
 | $\bigl| |x+1|-|x-1|\bigr|$ |
 | $$ \Bigl(\sum_{k=1}^n x^k\Bigr)^2 $$ |
К сожалению, команды для явного указания размера ограничителя имеют одну неприятную особенность: если " основной шрифт" документа крупнее, чем кегль 10 (иными словами, если указаны классовые опции 11pt или 12pt — , то может случиться так, что скобка, размер которой задан, например, командой \bigl, имеет точно такой же размер, как и скобка "в чистом виде". Чтобы избежать этой неприятности, надо подключить пакет amsmath: тогда команды наподобие \bigl будут работать корректно.
Смена шрифтов в формуле
По умолчанию все латинские буквы в формулах набираются курсивом. Что делать, если вам нужен другой шрифт?
В первой лекции мы приводили примеры смены шрифтов в тексте с помощью команд наподобие \bfseries или \itshape. В формулах, однако же, для этих целей надо использовать другие средства.
Пусть, например, вам нужна буква

 | $\mathbf P^n$ |
Если буква

Вот полный список начертаний символов в формулах, которые можно получить без подключения дополнительных стилевых пакетов:
 | $\mathbf x+y$ |
 | $\mathrm x+y$ |
 | $\mathtt x+y$ |
 | $\mathsf x+y$ |
 | $\mathcalT_X$ |
 | $\mathit\Gamma+y$ |
Команду \mathcal, вызывающую "каллиграфический" шрифт, можно применять только к прописным латинским буквам.
Команда \mathit дает одну из возможностей (и не лучшую, надо сказать) получить прописные греческие буквы в наклонном начертании. Дело в том, что если у вас подключен пакет amsmath, то команда \mathit работать откажется (по крайней мере, в некоторых версиях этого пакета). В этом случае для печати в формуле прописных греческих букв в наклонном начертании применяются специальные команды, в которых перед названием буквы стоит var:
 | \varGamma |
 | \varDelta |
 | \varTheta |
 | \varLambda |
 | \varXi |
 | \varPi |
 | \varSigma |
 | \varUpsilon |
 | \varPhi |
 | \varPsi |
 | \varOmega |
Как мог заметить читатель, команды наподобие \mathrm действуют только на непосредственно следующую букву. Если нужно, чтобы другим шрифтом была напечатана не одна буква, а несколько, надо все эти буквы взять в фигурные скобки:
 | Множество особенностей многообразия $X$ обозначается $X_{\mathrm{sing}}$. |
Все сказанное означает, что команда \mathrm и ей подобные принимают один обязательный аргумент — фрагмент формулы, который надо напечатать другим шрифтом. На первый взгляд, это противоречит сказанному на выше: ведь обязательный аргумент должен быть в фигурных скобках, а в конструкциях вроде \mathbf x никаких фигурных скобок нет.
Дело в том, что, в дополнение к сказанному ранее, действует еще одно правило: если после имени команды, принимающей обязательный аргумент, следует не открывающая фигурная скобка, а буква, то в качестве аргумента будет воспринята именно эта буква. Так что можно было бы писать и \mathbf{x} вместо \mathbf x, но так обычно не делают, чтобы не нажимать лишний раз на клавиши.
Если подключить стилевой пакет amsfonts или amssymb, то в математических формулах можно использовать еще два шрифта: ажурный (






 | Алгебра $\mathfrak{sl}_2(\mathbb C)$ играет особую роль в теории представлений. |
Наконец, есть возможность использовать в формулах вариант рукописного шрифта, в котором буквы имеют более изысканные очертания:






Для этого надо подключить стилевой пакет \euscript; команда, задающая этот шрифт, называется \EuScript.
Теперь, когда вы знаете, как печатать символы в формулах прямым шрифтом, может возникнуть искушение восполнить отсутствие в стандартном комплекте LaTeX'а команды, дающей функцию

 | В формуле $\mathrm{tg} x$ буква $x$слишком близка к знаку тангенса. А вот в формуле $\sin x$ пробелы правильные. |
Если вам хочется узнать, почему все так получается, прочтите разд."Снова об интервалах и формулах".
Если вы хотите включить в формулу какой-либо текст, то одной команды \mathrm для этого также недостаточно: любой текст, заключенный между знаками доллара, пусть даже он набирается прямым шрифтом, TeX рассматривает как часть математической формулы, и в соответствии с этим игнорирует те пробелы, которые ставите вы, и расставляет пробелы по собственным правилам:
 | $$ \sqrt{x^3}=x \mathrm{для всех} x. $$ |
Остается только отметить, что ажурный и готический шрифты, о которых шла речь сейчас, можно использовать только в формулах, и набирать с их помощью обычный текст невозможно (так же, как невозможно набирать греческий текст с помощью команд \alpha, \beta и т.д.).
Кроме описанного выше (и рекомендуемого нами) способа переключения шрифтов в формулах, в LaTeX'е пока сохраняется (ради совместимости с LaTeX'ом 2.09) еще один способ, с которым можно ознакомиться из приведенной ниже таблицы.
| \mathrm x+y | {\rm x}+y |  |
| \mathbf x+y | {\bf x}+y |  |
| \mathsf x+y | {\sf x}+y |  |
| \mathtt x+y | {\tt x}+y |  |
| \mathcal T_X | {\cal T}_X |  |
Снова об интервалах в формулах
Сейчас мы обсудим вкратце, какими правилами руководствуется TeX при расстановке интервалов в математических формулах. В стандартных ситуациях мы об этом не задумываемся, а полностью доверяем LaTeX'у. То, о чем мы будем говорить, пригодится, если мы пользуемся в формулах сложными конструкциями (например, конструируем знак двойного интеграла из двух знаков интеграла и "отрицательных пробелов", и при этом не хотим подбирать верные интервалы экспериментально.
При наборе формулы TeX рассматривает ее как состоящую из частей одного из следующих типов:
| Обыкновенный символ | например, \alpha |
| Бинарная операция | |
| Бинарное отношение | |
| Математический оператор | |
| Подформула | например, {x^2} |
| Знак препинания | , или ; или \colon или \ldotp |
| Скобка |
Здесь подформула — это любой фрагмент формулы, заключенный в фигурные скобки. Команда \colon задает двоеточие, рассматриваемое как знак препинания (двоеточие, набранное непосредственно, рассматривается TeX'ом как знак бинарного отношения), а команда \ldotp — точку, рассматриваемую как знак препинания (точка, набранная непосредственно, рассматривается как обыкновенный символ). К бинарным отношениям (с точки зрения TeX'а) относятся также все стрелки (\стр{arrows}) и фрагменты формул, создаваемые командой \stackrel. При расстановке пробелов в формуле TeX руководствуется тем, к какому из перечисленных типов относятся ее составные части: символы бинарных операций окружаются "средними пробелами" (теми, что вручную задаются командой \:), а символы бинарных отношений — "толстыми" пробелами (вручную, как мы помним, толстый пробел задается командой \;); впрочем, в стилях для индексов и индексов к индексам (см. предыдущий раздел) эти пробелы опускаются; после знака препинания в большинстве случаев ставится "тонкий" пробел, и т.д2) Подформула (т. е. фрагмент формулы, заключенный в фигурные скобки) рассматривается TeX'ом почти так же, как обычный символ:
 | Сравните $2+3$ и $2{+}3$: во втором случае знак плюс является подформулой, а не символом бинарной операции. |
Кстати, с этим приемом (поставить фрагмент формулы в фигурные скобки, чтобы он рассматривался как обычный символ) мы уже сталкивались ранее, когда обсуждали, как задать в TeX'е десятичную дробь.
Мы не будем вдаваться в точные правила расстановки пробелов (они перечислены в книге [2]). Для нас сейчас важнее то, что TeX можно заставить рассматривать любой фрагмент формулы как бинарную операцию, бинарное отношение или математическую операцию: для этого надо применить команды \mathbin, \mathrel или \mathop соответственно. Вот примеры того, как работают эти команды.
Иногда возникает нужда в символе

 | Хотелось бы, чтобы в формуле $E\hat{\otimes}F$ были такие же пробелы, как и в формуле $E\otimes F$. |

 | В формуле $E\mathbin{\hat{\otimes}}F$ пробелы такие же, как и в $E\otimes F$. |

Типичный пример использования команды \mathop - определение имени операции, записываемой прямым шрифтом. Обозначения такого типа встречаются в математических текстах очень часто, и набора команд для них, предусмотренного LaTeX'ом , вполне может не хватить; в этом случае, чтобы получить на печати, скажем,

$\mathop{\mathrm{Ext}}\nolimits^1(E,F)$ Здесь \mathop необходимо для того, чтобы между


 | Сравните $\sin x$ и $\mathrm{sin}x$. |
А вот пример, когда TeX' у надо объяснить, что некоторый сложный символ есть символ математического оператора. Пусть нам понадобилась формула

 | $$ \sum'_{x\in\Gamma}f(x). $$ |
$$ \sum^\prime_{x\in\Gamma}f(x). $$ и в этой записи штрих рассматривается как предел суммирования. Не будем, однако, отчаиваться, а просто создадим новый оператор "сумма со штрихом":
$$ \mathop{{\sum}'}_{x\in\Gamma}f(x). $$ Можете проверить, что на сей раз все получается как надо. В этой записи очень существенно, что \sum взято в фигурные скобки: благодаря этому символ, генерируемый командой \sum, рассматривается TeX'ом просто как подформула, поэтому и штрих после него стоит где положено, а не там, где бывают пределы суммирования. Вся подформула "{\sum}" передается в качестве аргумента команде \mathop, благодаря чему наш новый символ "сумма со штрихом" рассматривается как математический оператор и пределы суммирования (в выключной формуле) ставятся у него, где положено.
Здесь опять разумно создать сокращенное обозначение, которое заменяло бы эту громоздкую запись.
Таблицы спецзнаков с комментариями
В этом разделе мы перечислим математические знаки, предоставляемые LaTeX'ом. Знаков этих очень много, поэтому разобьем их на несколько групп. Это разбиение делается не только для удобства восприятия: как мы увидим в разд. "Снова об интервалах и формулах", расстановка интервалов в формулах зависит от того, к какой группе (бинарная операция, бинарное отношение, обыкновенный символ и т.д.) относится математический символ.
Тонкая настройка
В этом разделе мы рассмотрим некоторые более изысканные вопросы, связанные с набором математических формул. Рекомендуем читателям, не являющимся полиграфистами, пропустить в этом разделе мелкий шрифт (хотя бы при первом чтении).
Вертикальные отбивки вокруг выключных формул
За размер вертикальных отбивок, автоматически создаваемых TeX'ом вокруг выключных формул, отвечают следующие TeX'овские параметры:
| \abovedisplayskip | \abovedisplayshortskip | перед формулой |
| \belowdisplayskip | \belowdisplayshortskip | после формулы |
В каждой из этих пар второй параметр относится к случаю, когда и формула, и соседняя с ней строка текста коротки (в таком случае расстояние между формулой и текстом должно быть поменьше). Если вы хотите уменьшить эти отбивки, скажем, на 30%, напишите в преамбуле
\abovedisplayskip=.7\abovedisplayskip(и аналогично для трех остальных параметров).
Можно не только пропорционально изменять отбивки вокруг выключных формул, как в примере выше, но и присваивать этим интервалам конкретные значения. При этом следует иметь в виду следующее обстоятельство. Интервалы, создаваемые между текстом и формулами, обладают определенной растяжимостью, что помогает TeX'у выравнивать страницы по высоте (говоря на TeX'ническом языке, эти интервалы являются "клеем"), и присваивая абсолютное значение таким интервалам, желательно также задавать их растяжимость и сжимаемость; (более подробно — разд. "Клей" лекции 8 по поводу того, как это делается.
Включение текста в формулы
В математическую формулу можно включить фрагмент обычного текста с помощью LaTeX'овской команды \mbox. В следующем примере продемонстрировано, как это можно сделать; в нем используется еще команда \qquad, делающая в тексте или формуле пробел размером 2em ; подробнее по поводу команд, создающих пробелы в формулах, см. разд. "Пробелы вручную"; по поводу команд, создающих пробелы в тексте, см. разд. "Установка прромежутков вручную ".лекция 3
 | $$ \sqrt{x^3}=x\qquad \mbox{для всех }x. $$ |
Аргумент команды \mbox обрабатывается TeX'ом как обычный текст: пробелы не игнорируются, слова набираются не математическим курсивом, а тем же шрифтом, который был текущим перед началом формулы (у нас это был обычный прямой шрифт; если вы хотите, чтобы шрифт был другой, можно внутри аргумента команды \mbox дать команду смены шрифта в тексте). Весь текст, являющийся аргументом команды \mbox, будет напечатан в одну строку. В приведенном примере мы оставили пробел перед закрывающей фигурной скобкой, чтобы обеспечить пробел между текстом и формулой (фрагмент текста, созданный командой \mbox, рассматривается TeX'ом как одна большая буква; пробел в формуле между "буквой", содержащей текст из \mbox, и буквой

На самом деле можно было бы написать даже так:
$$ \sqrt{x^3}=x\qquad\mbox{для всех $x$.} $$Аргумент команды \mbox рассматривается как текст, но этот текст вполне может, в свою очередь, содержать формулы!
При включении текста в формулы с помощью команды \mbox важно иметь в виду вот что. Как читатель, видимо, уже заметил, в математических формулах верхние и нижние индексы, числитель и знаменатель дробей, созданных с помощью команды \frac, и тому подобные фрагменты набираются более мелким шрифтом, чем остальная часть формулы. Однако в тексте, созданном с помощью \mbox, размер шрифта не изменится, в какую бы часть формулы этот текст не попал. Если вас это не устраивает, подключите стилевой пакет \amsmath и воспользуйтесь командой \text вместо \mbox\,: тогда включенный в формулу текст будет правильно менять размеры в степенях и индексах, а если аргумент команды \text сам, в свою очередь, содержит формулу, то размеры символов в этой формуле будут выбраны более правильно, чем при использовании \mbox.
Вне математических формул команду \text использовать нельзя.
Команда \mbox еще встретится нам в следующей лекции, когда речь пойдет о предотвращении переносов в словах; более подробно мы ее рассмотрим в лекции 8.
